Fleischmann/Pons: Electrochemically induced nuclear fusion of deuterium - 1989
Elektrochemisch induzierte Kernfusion von Deuterium
Martin Fleischmann
Stanley Pons
(Eingegangen am 13. März 1989; in überarbeiteter Form am 22. März 1989)

Einleitung
Schon seit mehr als 100 Jahren untersucht man das ungewöhnliche Verhalten von in Palladium elektrolytisch erzeugtem Wasserstoff. Zuletzt wurden diese Untersuchungen auch auf Deuterium und Tritium ausgedehnt[1]. Bei der Freisetzung von Deuterium aus alkalischen Lösungen auf der Basis von schwerem Wasser müssen die folgenden Reaktionsschritte berücksichtigt werden:
| [math]D_2O + e^- \to D_{ads} + OD^-[/math] | (i) |
| [math]D_{ads} + D_2O + e^- \to D_2 + OD^-[/math] | (ii) |
| [math]D_{ads} \to D_{lattice}[/math] | (iii) |
| [math]D_{ads} + D_{ads} \to D_2[/math] | (iv) |
Es ist allgemein bekannt, dass bei negativen Potenzialen von bis zu + 50 mV auf der reversiblen Wasserstoffskala sich das Gitter in der β-Phase befindet, der Wasserstoff in Form von Protonen vorliegt (wie sich dies anhand der Wanderung in einem elektrischen Feld zeigt) und dabei sehr mobil ist (D = 10-7 cm2 s-1 für die α-Phase bei 300 K).
Der gesamte Reaktionsweg der Entwicklung von D2 besteht aus den Schritten (i) und (ii)[2], so dass das chemische Potenzial von gelöstem D+ normalerweise durch die relativen Raten dieser beiden Schritte bestimmt wird. Die Schaffung eines negativen Überpotenzials an der ausgehenden Schnittstelle der Palladium-Membranelektroden zur Freisetzung von Wasserstoff an der eingehenden Schnittstelle[3] [bestimmt durch die Bilanz aller Schritte (i) bis (iv)] zeigt, dass das chemische Potenzial auf hohe Werte angehoben werden kann. Unsere eigenen Experimente mit Palladium-Diffusionsröhrchen haben gezeigt, dass Werte von bis zu 0,8 eV ohne weiteres erreicht werden können[4] (Werte von bis zu 2 eV sind möglich). Die astronomische Größenordnung dieses Wertes lässt sich leicht nachvollziehen: Versuche, dieses Niveau über die Kompression von D2 [Schritt (iv)] zu erreichen, würden Drücke von über 1026 atm erfordern. Und selbst bei dieser hohen Kompression wird kein D2 gebildet, d. h. der s-Zustand der Elektronendichte um die Kerne ist sehr gering und die Elektronen sind Teil der Bandstruktur des Gesamtsystems. Eine Besonderheit, die von besonderem Interesse ist und die Anlass für die vorliegende Untersuchung war, ist der sehr hohe H/D-Trennungsfaktor für absorbierten Wasserstoff und Deuterium (siehe Abb. 4 und 6 von Ref. 2). Dies kann nur damit erklärt werden, dass sich die H+ und die D+ im Gitter wie klassische Oszillatoren (möglicherweise als delokalisierte Spezies) verhalten, d. h. sie müssen sich in sehr flachen Potenzialtöpfen aufhalten. In Anbetracht der sehr hohen Kompression und der Beweglichkeit der gelösten Spezies muss es daher zu einer signifikanten Anzahl von Nahkollisionen kommen, und man kann sich die Frage stellen: Würde eine Kernfusion von D+ wie etwa eine
| [math]{^2D} + {^2D} \to {^3T} (1.01 \; MeV) + {^1H} (3.02 \; MeV)[/math] | (v) |
oder
| [math]{^2D} + {^2D} \to {^3He} (0.82 \; MeV) + n (2.45 \; MeV)[/math] | (vi) |
unter diesen Bedingungen realisierbar sein?
Die Experimente
In der hier vorgestellten Studie wurde D+ galvanostatisch in Pd-Proben in Form von Platten, Stäben und Würfeln aus 0,1 M LiOD in 99,5 % D2O + 0,5 % H2O-Lösungen verdichtet. Die Elektrodenpotenziale wurden in Relation zu einer bis zum α-β-Phasengleichgewicht geladenen Pd-D-Referenzelektrode gemessen. Es wird hier über mehrere Arten von Experimenten berichtet:
(1) Kalorimetrische Messungen von Wärmebilanzen bei niedrigen Stromdichten (= 1,6 mA cm-2) wurden mit einer 2 mm × 8 cm × 8 cm großen Pd-Plattenkathode, umgeben von einer großen Pt-Platten-Gegenelektrode, durchgeführt. Die Messungen wurden in Dewarzellen durchgeführt, die in einem großen Wasserbad von konstanter Temperatur (300 K) gehalten wurden, wobei die Temperatur innerhalb der Zelle und des Wasserbades mit Beckmann-Thermometern überwacht wurde. Das Schwerwasseräquivalent des Dewars und des Inhalts sowie die Rate der Abkühlungsverluste nach dem Newtonschen Gesetz wurden durch Zugabe von heißem D2O und durch die Überwachung der Abkühlungskurven bestimmt.
(2) Kalorimetrische Messungen bei höheren Stromdichten wurden mit Pd-Stäben von 1, 2 und 4 mm Durchmesser und 10 cm Länge durchgeführt, die von einer Pt-Drahtanode umgeben waren, welche auf einen Käfig aus Glasstäben aufgewickelt war. Die Dewars waren mit Widerstandsheizungen zur Bestimmung der Kühlverluste nach dem Newtonschen Gesetz ausgestattet; die Temperaturen wurden mit kalibrierten Thermistoren gemessen. Über Experimente mit Stäben von bis zu 2 cm Durchmesser wird an anderer Stelle berichtet [5]. Die Umwälzung in diesen Experimenten [und in den unter (1) aufgeführten] wurde, wo nötig, durch eine Gasdurchströmung mit elektrolytisch erzeugtem D2 erreicht. Messungen bei der höchsten hier berichteten Stromdichte (512 mA cm-2) wurden mit Stäben von 1,25 cm Länge durchgeführt; die in Tabelle 1 angegebenen Ergebnisse wurden auf die für Stäbe von 10 cm Länge umskaliert.
(3) Das Spektrum der vom Wasserbad emittierten γ-Strahlung als Folge der (n, γ)-Reaktion
| [math]{^1H} + n (2.45 \; MeV) = {^2D} + \gamma (2.5 \; MeV)[/math] | (vii) |
wurde mit Hilfe eines Natriumjodid-Kristallszintillationsdetektors und eines Nuclear Data ND-6 bestimmt, einem Spektrumanalysator für Hochenergiespektren. Das Spektrum wurde oberhalb des Wassers erfasst, das eine 0,8 cm × 10 cm große und bis zum Gleichgewicht aufgeladene Pd-Stabkathode unmittelbar umgibt. Die Korrektur des Hintergrunds erfolgte über die Subtraktion eines Spektrums über einem Becken (mit identischen Abschirmungsmaterialien), welches sich 10 m vom Wasserbad entfernt befand.
Der Neutronenfluss aus einer Zelle mit einer 0,4 × 10 cm großen Pd-Stabelektrode wurde mit einem Harwell Neutronendosis-Äquivalentratenmonitor des Typs 95/0949-5 gemessen. Die Zähleffizienz dieses Instruments, das nach dem Prinzip der Bonner-Kugel arbeitet, wurde für Neutronen von 2,5 MeV auf ≈ 2,4 x 10-4 geschätzt und war aufgrund der ungünstigen Konfiguration (der Stab befand sich direkt gegenüber dem mit BF3 befüllten Detektor) um einen Faktor von etwa 100 reduziert. Die Hintergrundzählung erfolgte durch Messungen in 50 m Entfernung von jenem Labor, in dem die Experimente durchgeführt wurden; beide Standorte befanden sich jeweils im Keller eines Neubaus, der mit 5 Stockwerken aus Beton überbaut ist. Angesichts der geringen Zähleffizienz erfolgte die Zählung über einen Zeitraum von 50 h. Messungen an einer 0,4 cm × 10 cm großen Stabelektrode, die mit 64 mA cm-2 betrieben wurde, ergaben eine Neutronenzahl, die dreimal so hoch war wie die der kosmischen Hintergrundstrahlung.
(4) Die Rate der Erzeugung und Anreicherung von Tritium wurde mit ähnlichen Zellen (Reagenzgläser, die mit Parafilm versiegelt waren) gemessen, die Pd-Stabelektroden mit einem Durchmesser von 1 mm und einer Länge von 10 cm enthielten. Messungen des reinen D/T-Trennfaktors wurden mit einer identischen Zelle und einer Pt-Elektrode mit einem Durchmesser von 1 mm und einer Länge von 10 cm durchgeführt (diese Messung diente als Blindwert, da die H/D-Trennfaktoren für Pd und Pt erfahrungsgemäß recht nahe beieinander liegen). Im Abstand von 2 Tagen wurden 1-ml-Proben des Elektrolyten entnommen, mit Kaliumhydrogenphthalat neutralisiert und der T-Gehalt mit dem Ready Gel Flüssigszintillations-„Cocktail“ und einem Beckman LS 5000 TD Zählsystem ermittelt. Die Zähleffizienz wurde unter Verwendung von Standardproben T-haltiger Lösungen bei etwa 45 % festgestellt. Das β-Zerfalls-Szintillationsspektrum wurde unter Verwendung des Zählsystems erfasst.
Bei allen diesen Experimenten wurde nach der Probenentnahme standardmäßig wieder 1 ml des Elektrolyten nachgefüllt. Verluste an D2O durch die Elektrolyse wurden bei diesen und allen anderen hier aufgezeichneten Experimenten allein durch die Zugabe von D2O kompensiert. Das Volumen der D2O-Zugaben wurde für alle Experimente protokolliert.
Bei allen hier dokumentierten Experimenten wurden sämtliche Anschlüsse in Kappen aus KEL-F eingepasst und die Kappen mit Parafilm an den Glasgefäßen abgedichtet.
Die Ergebnisse aus der Massenspektroskopie der entstandenen Gase sowie die vollständigen experimentellen Details aller Messungen werden an anderer Stelle veröffentlicht[5].
Die Ergebnisse
Die Experimente (1) und (2)
In den kalorimetrischen Experimenten lassen sich für die Raten der jouleschen Erwärmung untere und obere Grenzen festlegen, je nachdem, ob die Reaktionen (i), (ii) und (iv) durch die folgende Reaktion
| [math]4 \; OD^- \rightleftharpoons D_2O + O_2 + 4 \, e^-[/math] | (viii) |
an der Anode oder durch die Umkehrung der Reaktionen (i), (ii) und (iv) ausgeglichen werden. Im ersteren Fall ergibt sich die joulesche Erwärmung einfach aus dem Strom der Zelle, multipliziert mit der Spannung der Zelle (-1,54 V), wobei die Spannung von 1,54 V genau diejenige ist, bei der sich die Reaktionen (i), (ii) und (iv) im Gleichgewicht mit (viii) thermisch neutral verhalten: Irreversibilitäten in den Reaktionen der Elektrode und ohmsche Widerstandsverluste führen bezüglich der jouleschen Erwärmung zu identischen Ergebnissen. Wenn sich die Reaktionen (i), (ii) und (iv) an der Anode jedoch umkehren, und wenn die Umkehrung der Reaktion (viii) in gleicher Weise zu den Kathodenprozessen beiträgt, dann erhalten wir für die joulesche Erwärmung eine Obergrenze, die sich einfach aus dem Zellstrom, multipliziert mit der Zellspannung, ergibt.
Durch Langzeitexperimente konnten wir belegen, dass es sich bei den Mengen an D2O, die den Zellen zugeführt werden müssen, um deren Volumina konstant zu halten, um diejenigen handelt, die für die Reaktionen (i), (ii) und (iv) benötigt werden und die durch die Reaktion (viii) ausgeglichen werden. Darüber hinaus hat die Subtraktion der ohmschen Potenzialverluste für die Lösung jener Zelle, die die große Pt-Anode enthält, gezeigt, dass die Elektrolyse von D2O den dominanten Prozess darstellt, d. h. wir müssen davon ausgehen, dass die joulesche Erwärmung sich nahe der unteren Grenze befindet.
Tabelle 1
Erzeugung überschüssiger Enthalpie in Pd-Kathoden als Funktion der Stromdichte und der Größe der Elektrode
| Elektrodentyp | Abmessungen [cm] |
Stromdichte [mA cm-2] |
Rate der Überschusserwärmung [W] |
Spezifische Rate der Überschusserwärmung [W cm-3] |
|---|---|---|---|---|
| Stäbe | 0.1 × 10 | 8 | 0.0075 | 0.095 |
| 64 | 0.079 | 1.01 | ||
| 512a | 0.654a | 8.33 | ||
| 0.2 × 10 | 8 | 0.036 | 0.115 | |
| 64 | 0.493 | 1.57 | ||
| 512a | 3.02a | 9.61 | ||
| 0.4 × 10 | 8 | 0.153 | 0.122 | |
| 64 | 1.751 | 1.39 | ||
| 512a | 26.8a | 21.4 | ||
| Platte | 0.2 × 8 × 8 | 0.8 | 0 | 0 |
| 1.2 | 0.027 | 0.0021 | ||
| 1.6 | 0.079 | 0.0061 | ||
| Würfel | 1 × 1 × 1 | 125 | Warnung! Entzündung! Siehe Text | |
| 250 | ||||
a Gemessen an Elektroden mit einer Länge von 1,25 cm und umskaliert auf 10 cm.
Tabelle 1 zeigt die Ergebnisse für Experimente, bei denen die Auswirkungen der Elektrolytgeometrie, der Elektrodengröße, der Stromdichte (oder des Überpotentials), der Betriebsweise usw. untersucht wurden. Die Natur und das große Ausmaß der Effekte lassen sich aus den folgenden Beobachtungen ableiten:
(a) Die Erzeugung überschüssiger Enthalpie ist in hohem Maße abhängig von der angewandten Stromdichte (das heißt von der Größe der Verschiebung des chemischen Potenzials) und verhält sich proportional zum Volumen der Elektroden, sodass wir es hier mit einem Phänomen zu tun haben, das sich in der Masse aller Pd-Elektroden wiederfindet.
(b) Die Erzeugung von Enthalpie kann bei der Palladiumelektrode einen Wert von 10 W cm-3 überschreiten. Dies lässt sich für Experimentierzeiten von mehr als 120 h aufrechterhalten, bei denen typischerweise Wärme von mehr als 4 MJ cm-3 des Volumens der Elektrode freigesetzt wurde. Es ist unvorstellbar, dass dies auf etwas anderes als auf nukleare Prozesse zurückzuführen sein kann.
(c) In der Forschung zur thermonuklearen Fusion werden diese Effekte als ein Prozentsatz des Break-even ausgedrückt, wobei ein 100-prozentiger Break-even impliziert, dass der thermische Output gleich dem Input ist (unter Vernachlässigung der für den Gerätebetrieb erforderlichen Energie). Bei elektrochemischen Experimenten muss zusätzlich berücksichtigt werden, ob der Break-even nur auf der jouleschen Wärme basieren soll oder auf der gesamten Energie, die der Zelle zugeführt wird. Im letzteren Fall hängt die zugeführte Menge an Energie außerdem von der Art der Anodenreaktion ab. Tabelle 2 listet dazu drei derartige Kennzahlen auf, und es ist zu erkennen, dass sich daraus schon jetzt vernünftige Projektionen auf 1000 % ableiten lassen. Einige der Faktoren, die für ein Scale-up von Bedeutung sind, lassen sich bereits aus den Tabellen 1 und 2 ablesen.
Tabelle 2
Erzeugung von Überschussenthalpie in Pd-Stabkathoden, ausgedrückt als Prozentsatz der Break-even-Werte. Alle Prozentangaben beziehen sich auf 2D+2D-Reaktionen, d. h. keine Hochrechnung auf 2D+3T-Reaktionen
| Elektrodentyp | Abmessungen [cm] |
Stromdichte [mA cm-2] |
Überschusserwärmung des Break-even [%] | ||
|---|---|---|---|---|---|
| a | b | c | |||
| Stäbe | 0.1 × 10 | 8 | 23 | 12 | 60 |
| 64 | 19 | 11 | 79 | ||
| 512 | 5 | 5 | 81 | ||
| 0.2 × 10 | 8 | 62 | 27 | 286 | |
| 64 | 46 | 29 | 247 | ||
| 512 | 14 | 11 | 189 | ||
| 0.4 × 10 | 8 | 111 | 53 | 1224 | |
| 64 | 66 | 45 | 438 | ||
| 512 | 59 | 48 | 839 | ||
a % des Break-even, basierend auf der der Zelle zugeführten jouleschen Wärme und der Anodenreaktion 4 OD- → 2 D2O + O2 + 4 e-.
b % des Break-even, basierend auf der der Zelle zugeführten Gesamtenergie und der Anodenreaktion 4 OD- → 2 D2O + O2 + 4 e-.
c % des Break-even, basierend auf der der Zelle zugeführten Gesamtenergie und für eine Elektrodenreaktion D2 + 2 OD- → 2 D2O + 4 e- mit einem Zellpotential von 0,5 V.
d) Zur Bestimmung der Effekte ist einzig und allein D2O zum Einsatz gekommen. Bei der Projektion auf die Verwendung geeigneter Gemische aus D2O + DTO + T2O (wie in der Fusionsforschung üblich) sind daher thermische Überschüsse im Bereich von 105-106 % (auch bei fehlender Spinpolarisation) mit Enthalpiefreisetzungen von über 10 kW cm-3 zu erwarten. Wir müssen hier mitteilen, dass unter den Bedingungen des letzten Experiments, auch unter der alleinigen Verwendung von D2O, ein erheblicher Teil der Kathode geschmolzen (Schmelzpunkt 1544 °C), ein Teil von ihr verdampft und die Zelle samt Inhalt sowie ein Teil des Laborabzugs, in dem das Experiment untergebracht war, zerstört wurden.
Das Experiment (3)
Die Abbildung 1A zeigt die γ-Strahlenspektren, wie sie in Regionen oberhalb des Wasserbads neben den Elektrolysezellen aufgezeichnet wurden. Dieses Spektrum bestätigt, dass in den Elektroden durch die Reaktion (vi) tatsächlich Neutronen mit einer Energie von 2,45 MeV erzeugt werden. Diese γ-Strahlen werden über die Reaktion (vii) erzeugt. Wir halten fest, dass die Intensitäten der Spektren schwach sind. Und in Übereinstimmung damit liegt der aus den Messungen mit dem Dosimeter berechnete Neutronenfluss für eine 0,4 cm × 10 cm große Stabelektrode, welche mit 64 mA cm-2 polarisiert wurde, in der Größenordnung von 4 × 104 s-1.
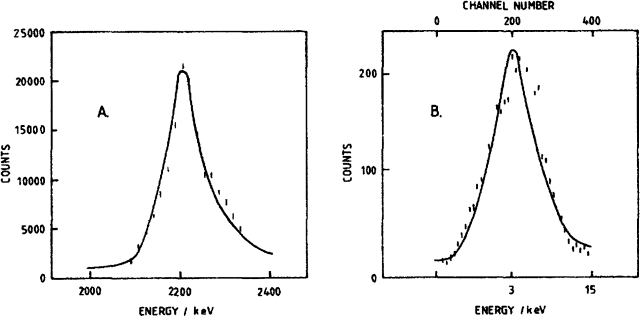
Das Experiment (4)
In Übereinstimmung mit diesem niedrigen Neutronenfluss deutet die Akkumulation im Elektrolyten auch auf eine niedrige Rate für die Reaktion (v) hin [die in Experimenten der Hochenergiephysik für etwas schneller als (vi) befunden wurde]. Der zeitabhängige Anteil von Tritium im Lösungsmittel zeigt sich wie folgt[5]
| [math]\alpha_T = \gamma_T \; exp \, { {-(1 + \lambda \, S_{D,T})Rt} \over {\gamma \, S_{D,T} \, N} } + [(1 + \lambda) \gamma_T + \beta / R] \, [/math] |
| [math]\times \, { {S_{D,T}} \over {(1 + \lambda \, S_{D,T})} } \left[ 1 - exp \, { {-(1 + \lambda \, S_{D,T} ) \, Rt} \over {\lambda \, S_{D,T} N} } \right][/math] | (1) |
wobei [math]\gamma_T[/math] den Anteil von [math]T[/math] in den Zuführungen an Elektrolyt bzw. Lösungsmittel darstellt, [math]\lambda R[/math] (Atome T s-1, hier 4 × 1011 Atome s-1) die Entnahmerate ist, die als zeitlich kontinuierlich angenommen wurde, [math]N[/math] die Gesamtzahl der Atome von [math]D[/math] im Dewar ist (14,6 × 1023), [math]S_{D,T}[/math] der D/T-Trennfaktor ist, [math]\beta[/math] die Rate der Kernreaktion in (v) ist (Ereignisse s-1) und [math]R[/math] die Rate der Elektrolyse ist, ausgedrückt als Atome [math]D[/math] s-1 (hier 1,24 × 1018 Atome s-1). Es ist zu erkennen, dass der Endwert von [math]\alpha_T[/math] für die Zelle mit der Pt-Kathode (für die wir [math]\beta_A = 0[/math] annehmen) wie folgt lautet
| [math]\alpha_T = \left[ (1 + \lambda) \, \gamma_T + \beta / R \right] \, { {S_{D,T}} \over {( 1 + \lambda \, S_{D,T} )} }[/math] | (2) |
Blindversuche mit Pt-Kathoden (die sehr ähnliche Trennfaktoren wie Pd aufweisen) ergaben eine geringe Akkumulation von DTO, so dass [math]S_{D,T}[/math] unter den Bedingungen unserer Experimente bei nahezu 1 liegt. In den Zellen mit den Pd-Kathoden reichert sich DTO in einem Ausmaß von etwa 100 dpm ml-1 des Elektrolyten an, und Abb. 1B zeigt, dass es sich bei der akkumulierten Spezies tatsächlich um Tritium handelt. Die Anwendung von Gleichung (2) zeigt dann, dass die Reaktion (v) in einem Ausmaß von 1–2 × 104 Atomen s-1 stattfindet, was im Einklang mit den Messungen des Neutronenflusses steht, sofern man den Unterschied in den Radien berücksichtigt. Andererseits würden die Daten zur Enthalpieerzeugung für die Reaktionen (v) und (vi) Raten im Bereich von 1011–1014 Atomen s-1 erfordern. Es ist offensichtlich, dass die Reaktionen (v) und (vi) nur ein kleiner Teil des gesamten Reaktionsschemas sind und dass noch weitere Kernreaktionen beteiligt sein müssen.
Diskussion
Wir sind uns darüber im Klaren, dass die hier berichteten Ergebnisse mehr Fragen aufwerfen, als sie Antworten liefern, und dass noch viel weitere Arbeit zu diesem Thema zu leisten ist. Die Feststellung, dass es in einer Pd-Kathode aus einem elektrochemisch komprimierten D+ zu einer Erzeugung von Neutronen und Tritium kommt, ist an sich schon ein sehr überraschendes Ergebnis und ganz offensichtlich besteht die Notwendigkeit, die Quantenmechanik von Elektronen und Deuteronen in solchen Wirtsgittern neu zu überdenken. Insbesondere muss die Frage gestellt werden: Ist es möglich, für die Reaktionen (v) und (vi) mit Clustern von Deuteronen (die sich vermutlich in den oktaedrischen Gitterpositionen befinden) bei typischen Energien von 1 eV eine Fusionsrate von 10-19 s-1 zu erreichen? Mit Experimenten an isotopisch substituierten Hydriden wohldefinierter Strukturen könnte diese Frage durchaus beantwortet werden.
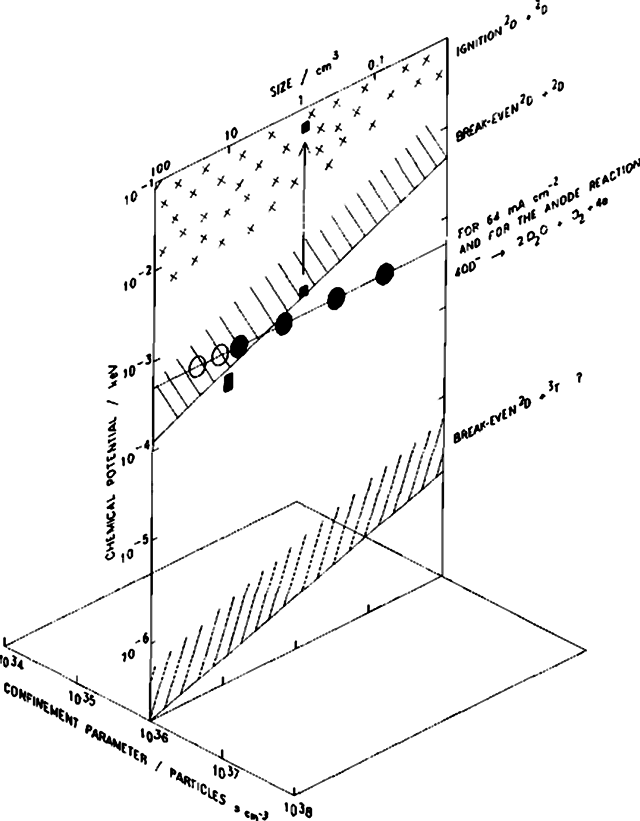
Die erstaunlichste Erkenntnis aus unseren Ergebnissen besteht jedoch darin, dass die Reaktionen (v) und (vi) nur einen relativ kleinen Teil des gesamten Reaktionsschemas ausmachen und dass der Großteil der Energiefreisetzung auf einen bisher unbekannten nuklearen Prozess oder auf mehrere solcher Prozesse zurückzuführen ist (vermutlich ebenfalls durch Deuteronen verursacht). Wir möchten die Aufmerksamkeit nochmals auf die außerordentlich starke Ausprägung der Effekte im Einschlussparameter-Diagramm von Abb. 2 lenken. Wir können feststellen, dass die Werte für den Einschlussparameter im Vergleich zur konventionellen Fusionsforschung (mit ihren hohen Teilchendichten und Lebensdauern zwischen 105 und 106 Jahren) extrem hoch sind, während das chemische Potenzial im Vergleich zum entsprechenden Parameter (T) in diesen Experimenten sehr niedrig ausfällt. Es liegt auf der Hand, dass derartige Diagramme für elektrochemische Experimente eine Erweiterung in die dritte Dimension erfordern, da die Ergebnisse in so starkem Maße vom Volumen der Elektroden abhängig sind (eine Erhöhung der Stromdichte verschiebt die Messpunkte in vertikaler Richtung). Wir weisen nochmals darauf hin, dass die bereits durchgeführten Experimente sich nahe am Break-even-Punkt befinden. Weitere Arbeiten zur Erweiterung der Elektrodenabmessungen (sowie zur Ergründung der Natur der für die Enthalpieentwicklung verantwortlichen Prozesse) sind im Gange. Schließlich mahnen wir bei derartigen Experimenten zu äußerster Vorsicht: Eine plausible Interpretation des Experiments unter Verwendung der Pd-Würfelelektrode geht in Richtung einer Entzündung. Die Projektion der Werte aus den Tabellen 1 und 2 auf noch extremere Voraussetzungen deutet darauf hin, dass so etwas durchaus möglich sein könnte.
Danksagung
Wir danken der Firma Johnson Matthey PLC, die uns die Edelmetalle für dieses Projekt leihweise zur Verfügung gestellt hat.
Referenzen
- ↑ W. M. Mueller, J. P. Blackledge and G. G. Libowitz: Metal Hydrides, Academic Press, New York, 1968; G. Bambakadis (Hrsg.), Metal Hydrides, Plenum Press, New York, 1981.
- ↑ B. Dandapam and M. Fleischmnann, J. Electroanal. Chem., 39 (1972) 323.
- ↑ A. N. Frumkin and N. A. Aladzhalova, Acta Physicochim. U.R.S.S., 19 (1944) 1.
- ↑ M. Fleischmann and S. Pons, unpublished results.
- ↑ 5,0 5,1 5,2 M. Fleischmann, M. Hawkins and S. Pons, J. Electroanal. Chem., to be submitted.
