Der E-Cat SK und Partikelwechselwirkungen mit großer Reichweite (2022)

Von Andrea Rossi

Grundlage

Es handelt sich hier um eine umfassende Überarbeitung des originalen Vorabdrucks, welche am 24. Dezember 2020 vorgenommen wurde.
Letzte Aktualisierung: 21. Oktober 2022
Zum Originaldokument

Zusammenfassung

Es werden einige theoretische Modelle vorgestellt, die die mögliche Bildung dichter exotischer Elektronencluster im E-Cat SK untersuchen. Ferner werden einige Überlegungen zur wahrscheinlichen Rolle von Casimir-, Aharonov-Bohm- und kollektiven Effekten bei der Bildung solcher Strukturen angestellt. Es wird eine Lagrange für eine relativistische Wechselwirkung auf der Grundlage eines reinen elektromagnetischen Elektronenmodells vorgestellt, die die Möglichkeit der Existenz von Ladungsaggregaten mit sehr niedriger Entropie nahelegt und dabei die primäre Rolle elektromagnetischer Potenziale in diesen Clustern herausstellt. Die Bildung solcher Cluster steht möglicherweise im Zusammenhang mit einer lokal begrenzten Vakuumpolarisation, welche durch eine schnelle radiale Ladungsverschiebung hervorgerufen wird. Die Bildung dieser dichten Elektronencluster gilt als wahrscheinlicher Vorläufer für die Bildung von Protonen-Elektronen-Aggregaten im Pikometermaßstab, was die Bedeutung der Plausibilitätsprüfung spezieller Elektron-Nukleon-Wechselwirkungen unterstreicht, wie sie bereits in nahegelegt wurde. Die beobachtete Abhängigkeit von Isotopen einer bestimmten Spektrallinie im Bereich des sichtbaren Spektrums des E-Cat-Plasmas deutet auf die Existenz einer speziellen Proton-Elektron-Wechselwirkung im Spektralbereich der Compton-Wellenlänge von Elektronen hin.

Einführung

Die E-Cat-Technologie stellt für die konzeptionellen Grundlagen der modernen Physik eine ernsthafte und zugleich interessante Herausforderung dar. Für das Verständnis dieser Technologie erweist sich insbesondere die Erforschung von Partikelwechselwirkungen über große Distanzen als vielversprechend. Im Abschnitt „Nuclear Reactions in Distant Collisions“ hebt E. P. Wigner deren Bedeutung für die nuklearen Transferreaktionen hervor: „Die Tatsache, dass Kernreaktionen des Typs [math]Au^{197} + N^{14} \to Au^{198} + N^{13}[/math] sich in Energiebereichen ereignen, in welchen sich die kollidierenden Kerne noch nicht einmal berühren, stellt eine interessante, wenn auch wenig beachtete Entdeckung dar“. In der jüngeren Vergangenheit wurde in dem Artikel „Nucleon polarizability and long range strong force from [math]\sigma I = 2[/math] mesonexchange potential“ eine mögliche Doppelrolle der Elektronen im Rahmen von Fernwechselwirkungen vermutet: „Mit anderen Worten, befassen sich die beiden Ansichten mit der Rolle der Elektronen. Die eine besteht darin, das Nukleon zu tragen, und die andere darin, für das Nukleon ein Fernwirkungspotenzial aufzubauen“.

In dieser Arbeit zeigen wir auf, dass in einem relativ großen Bereich zwischen atomarer und nuklearer Skala, also in der gleichen Größenordnung wie die der Compton-Wellenlänge der Elektronen, die Auswirkungen der magnetischen Kraft, der Casimir-Kraft sowie des Quantenvakuums bzw. der virtuellen Teilchen nicht außer Acht gelassen werden dürfen. Insbesondere zeigen wir in Abschnitt 1, dass die Coulomb-Abstoßung zwischen den Elektronen in bestimmten geometrischen Konfigurationen durch die Casimir-Kraft über eine Distanz von vier reduzierten Compton-Wellenlängen ausgeglichen werden kann. Zu einer möglichen Rolle der Casimir-Kräfte im Rahmen der E-Cat-Technologie hatte zum ersten Mal Professor Sven Kullander während unserer Diskussionen im Jahr 2013 den Anstoß gegeben. In Erweiterung des Kernkraftmodells nach N. D. Cook, V. Dallacasa und P. Di Sia, was auf der magnetischen Anziehung zwischen den Nukleonen beruht, auf die Leptonen sowie unter der Voraussetzung, dass es sich bei der Viererdistanz zwischen den Ladungen in der Minkowski-Raumzeit um einen lichtartigen Vektor handelt, wird in Abschnitt 2 ein mögliches Gleichgewicht zwischen der magnetischen und der Coulomb-Kraft vorgestellt. Dazu wird eine relativistische Lagrange zur Wechselwirkung entwickelt, welche die Möglichkeit solcher kohärenten Aggregate von niedriger Entropie nahelegt. In Abschnitt 3 wird die Hypothese aufgestellt, der zufolge eine relativ begrenzte Elektronenenergie-Verteilungsfunktion (EEDF) eine Vorbedingung dafür bildet, dass es zur Bildung solcher kohärenten Aggregate kommen kann. In Abschnitt 4 wird ein Mechanismus vorgestellt, der die Nutzung der Nullpunktsenergie innerhalb der E-Cat-Technologie ermöglichen könnte. In Abschnitt 5 werden die dichten Elektronencluster als eine wahrscheinliche Vorstufe zur Bildung von Protonen-Elektronen-Aggregaten im Pikometerbereich vorgestellt. Dieser letzte Abschnitt befasst sich zudem auch mit der spektroskopischen Signatur dieser Strukturen. Abschnitt 6 enthält eine kurze Beschreibung des Versuchsaufbaus, während Abschnitt 7 die Berechnung der E-Cat SK-Leistung wiedergibt.

1. Die Ladungscluster und die Casimir-Kraft

Puthoff und Piestrup schlagen in ihrer Arbeit „Charge confinement by Casimir force“ als mögliche Ursache für die von K. Shoulders und anderen Forschern beobachtete Ladungskonzentration hoher Dichte den „Vakuumdruck“ vor, der 1948 von H. B. G. Casimir vermutet und 1996 von S. K. Lamoreaux experimentell nachgewiesen wurde. Um die Coulomb-Abstoßung der Elektronen durch den Vakuumdruck in einer kugelförmigen Schalenverteilung von [math]N[/math] Elektronen zu kompensieren, hat Puthoff einen kritischen Wert für den Kugelradius [math]R_N[/math] ermittelt:

[math]R_N \approx \large\frac{\hbar \sqrt{N}}{2 m_e c} = \large\frac{c \sqrt{N}}{2 \omega_e} = \large\frac{r_e \sqrt{N}}{2}[/math]

(1)

worin [math]r_e = c / \omega_e = \lambda_e / 2 \pi[/math] die reduzierte Elektronen-Compton-Wellenlänge darstellt. Dieser Wert ergibt sich aus der Compton-Winkelfrequenz [math]\omega_e = m_ec^2 / \hbar[/math] als Grenzfrequenz für Elektron-Vakuum-Wechselwirkungen unter der Annahme einer spektralen Energiedichte [math]\rho ( \omega )[/math] für das Vakuum:

[math]\rho (\omega) = \large\frac{\hbar \omega^3}{2 \pi^2 c^3} \, d \omega[/math]

Für einen Ladungscluster von [math]N = 10^{11}[/math] Elektronen beträgt die berechnete Clustergröße [math]D[/math] näherungsweise [math]D = 2R_N \approx 0,12 \, \mu m[/math], ein Wert, der nicht allzu weit von der typischen Ladungsclustergröße nach Shoulders entfernt ist. Der Elektronenabstand [math]d_E[/math] in der Kugelschale, der das elektrostatische Potential minimiert, kann in groben Zügen wie folgt approximiert werden:

[math]d_E \approx \sqrt{\large\frac{4 \pi R^2_N}{N}} = \sqrt{\pi} r_e \approx 1,78 \, r_e \approx 0,68 \cdot 10^{-12} \; m[/math]

(2)

Interessanterweise handelt es sich bei diesem Abstand nicht um eine Funktion von [math]N[/math], sondern um einen konstanten Wert, welcher die gleiche Größenordnung aufweist wie die reduzierte Compton-Wellenlänge des Elektrons [math]r_e = \lambda_e / 2 \pi \approx 0,38 \cdot 10^{-12} \, m[/math]. In dieser Größenordnung sollte das Elektron nicht als punktförmiges Teilchen beschrieben werden, auch nicht in einer ersten Näherung. Zur Bewertung des Casimir-Effektes in freien Elektronenclustern ist daher ein detaillierteres und realistischeres Elektronenmodell zu bevorzugen.

Ein interessanter Ansatz in dieser Richtung wird von J. Maruani in seinem Aufsatz „The Dirac Electron and Elementary Interactions“ verfolgt. Um die Casimir-Kraft zwischen Elektronen zu berechnen, schlägt Maruani vor, die Formel für die Casimir-Kraft [math]F_C[/math] pro Flächeneinheit [math]A[/math] auf den „Idealfall perfekter Platten im perfekten Vakuum bei 0 Kelvin“ anzuwenden:

[math]\large\frac{F_C (d)}{A} = \large\frac{\pi^2 \hbar c}{240 \, d^4}[/math]

(3)

worin [math]d[/math] den Abstand zwischen den Platten und [math]c[/math] die Lichtgeschwindigkeit im Vakuum angibt. Maruani geht von einem Zitterbewegung-Elektronenmodell aus, bei dem die reduzierte Compton-Wellenlänge dem „Durchmesser“ des Elektrons entspricht. In diesem Fall wird die „Plattenfläche“ in (3) zu [math]A = \pi (\lambda_e / 4 \pi)^2[/math] , wodurch die anziehende Casimir-Kraft [math]F_C \, (d)[/math] zwischen Elektronen berechnet und mit der Coulomb-Abstoßungskraft [math]F_e \, (d)[/math] verglichen werden kann:

[math]F_C \, (d) = \large\frac{\pi \hbar c \lambda^2_e}{3840 \, d^4}[/math]	(4)
[math]F_e \, (d) = \large\frac{1}{4 \pi \varepsilon_0} \large\frac{e^2}{d^2}[/math]	(5)

Diesem Ansatz zufolge gleicht die Casimir-Kraft bei einem Abstand von etwa [math]d_b \approx 2^{\lambda_e} / 2 \pi \approx 0,77 \cdot 10^{-12} \; m[/math] die Coulomb-Abstoßung aus – einem Wert, der nahe dem von zwei reduzierten Compton-Wellenlängen liegt (siehe die Abbildung 1 in ).

Nach einem anderen Zitterbewegung-Elektronenmodell lässt sich das Elektron durch eine Stromschleife mit dem Radius [math]r_e[/math] beschreiben, welche durch eine mit Lichtgeschwindigkeit rotierende Ladungsverteilung hervorgerufen wird. Diese Stromschleife wird als Ursprung von Masse, Trägheit, Drehimpuls, Spin sowie des magnetischen Impulses des Elektrons angesehen. In diesem Fall ist die vom zbw-Strom eingeschlossene Fläche [math]A = \pi (\lambda_e / 2 \pi)^2 = \pi r^2_e[/math] – ein Wert, der viermal so groß ist wie der von Maruani benutzte, und folglich kann die Casimir-Kraft einen viermal so großen Wert erreichen wie der in (4) angegebene. Mit dieser größeren Fläche wird die Coulomb-Abstoßung in einem Abstand [math]d_b \approx 4^{\lambda_e} / 2 \pi \approx 1,54 \cdot 10^{-12} \; m[/math] ausgeglichen, so wie in Abbildung 1 dargestellt, in der die angenommene Casimir-Kraft zwischen zwei Elektronen zusammen mit der Coulomb-Kraft sowie einer magnetischen Kraft, welche die Elektronen als zwei parallel ausgerichtete Stromschleifen betrachtet, in einer logarithmischen Skala aufgetragen ist. Das Konzept einer internen schnellen Bewegung (Zitterbewegung) mit Lichtgeschwindigkeit in den Elektronen findet sich in der Vorlesung von P. A. M. Dirac anlässlich der Verleihung des Nobelpreises.

Abbildung 1: Die Entwicklung der Casimir-, der Coulomb- und
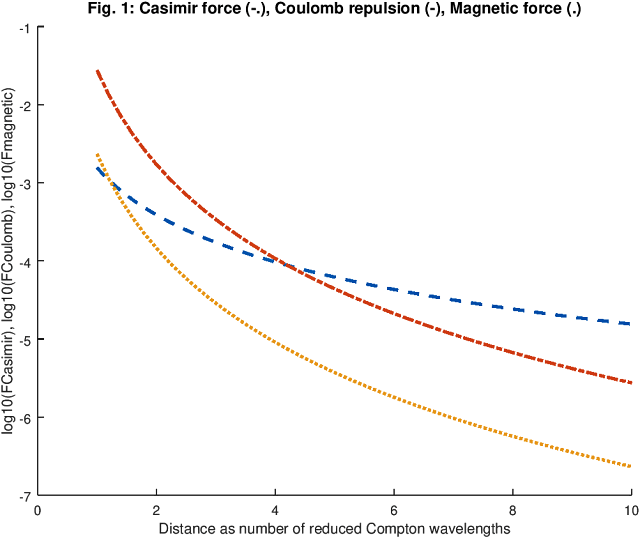
der magnetischen Kräfte als Funktion des Abstandes.

2. Ladungscluster und magnetische Wechselwirkungen

2.1. Raumladung, Vakuumpolarisation und virtuelle Teilchen

Einen wichtigen Effekt in Vakuumröhren stellt die sogenannte „Raumladung“ dar. Dieser Name bezieht sich auf die spontane Bildung einer Elektronenwolke um eine im Vakuum erhitzte Kathode. Obwohl dieser Effekt seit den Anfangsjahren der Vakuumröhrentechnologie bekannt ist und genutzt wird, steht für ihn keine klar definierte Theorie zur Verfügung. Die Aussage stützt sich vielmehr auf die Beobachtung, nach der die Bildung einer stabilen Raumladung durch die Coulomb-Abstoßung zwischen freien Elektronen eigentlich verhindert sein sollte. In seinem US-Patent 6465965 schlägt L. Nelson als Grund für diese weitreichende elektrostatische Abschirmung eine mögliche Vakuumpolarisation vor, die als Folge der durch die Heisenbergsche Unschärferelation vorhergesagten Fluktuationen des Quantenvakuums aus der Erzeugung und Annihilation virtueller Ladungspaare hervorgeht. Die Lebensdauer solcher Teilchen-Antiteilchen-Paare steht in umgekehrtem Verhältnis zu ihrer Massenenergie, doch im Laufe ihrer überaus kurzen Existenz können sie sich wie die Ladungen in einem Festkörperdielektrikum eines Kondensators verhalten, welche die für die Akkumulation einer Ladung in den Kondensatorplatten erforderliche Spannung aufgrund der Abschirmung des elektrischen Feldes verringern. Die Entstehung dieser virtuellen Teilchen wird durch die hohe Dichte an zulässigen Energiezuständen im Vakuum begünstigt und durch die relativ geringe Anzahl an zulässigen Zuständen in einem gewöhnlichen metallischen Leiter wieder eingeschränkt. Laut Nelson lässt sich diese Differenz ausnutzen, um auf diese Weise eine makroskopische Spannung zu erzeugen und einen Energiegewinn zu realisieren. Alternative Hypothesen, die auf selbstorganisierenden Zitterbewegung-Elektronenphasen im Vakuum und auf der Lorentzkraft basieren, sind jedoch ebenso möglich, wie in den nächsten Unterabschnitten gezeigt werden soll.

In jedem Fall handelt es sich bei der Fernwechselwirkung zwischen den Elektronen in der Raumladung um ein Phänomen, das es verdient, in ernsthafter Weise studiert und untersucht zu werden.

2.2. Die Lorentzkraft und die Phasenkohärenz der Zitterbewegung

Nach verbindet sich mit dem Elektron ein magnetischer Fluss [math]\Phi_M = h / e[/math], der dem Verhältnis von Planck-Konstante [math]h[/math] und Elementarladung [math]e[/math] entspricht. Daher lässt sich eine mögliche Beteiligung der magnetischen Anziehung am Ladungseinschluss nicht a priori ausschließen. Wie Abbildung 1 zeigt, ist die magnetische Kraft nicht in der Lage, die Coulomb-Abstoßung zwischen zwei Elektronen, betrachtet man diese naiverweise lediglich als zwei parallel ausgerichtete Stromschleifen, zu kompensieren. An dieser Stelle muss jedoch daran erinnert werden, dass der Strom der Zitterbewegung durch eine Elementarladung [math]e[/math] erzeugt wird, die mit Lichtgeschwindigkeit [math]c[/math] entlang eines Umfanges rotiert, der der Compton-Wellenlänge des Elektrons entspricht, und dass sich die magnetische Anziehungskraft zwischen den Ladungen im selben Lichtkegel durch eine Rotationsphasenkohärenz erheblich verstärken kann.

In diesem Fall lässt sich die Kraft als Lorentzkraft [math]F_L[/math] berechnen, die auf eine Elementarladung wirkt, welche sich mit Lichtgeschwindigkeit bewegt. Deren Wert vermag die Coulomb-Abstoßung auszugleichen:

[math]F_L\, (d) = ecB \, (d) = \large\frac{\mu_o}{4 \pi} \cdot \large\frac{e^2c^2}{d^2} = \large\frac{1}{4 \pi \epsilon_0} \cdot \large\frac{e^2}{d^2}[/math]

(6)

worin

[math]B \, (d) = \large\frac{\mu_o e c}{4 \pi d^2}[/math]

(7)

die magnetische Flussdichte darstellt, die von einer weiteren Elementarladung erzeugt wird, welche sich mit Lichtgeschwindigkeit [math]c[/math] parallel dazu und mit einem Abstandsvektor [math]\vec{d}[/math] orthogonal zum Geschwindigkeitsvektor der Ladung bewegt.

In einem ähnlichen Ansatz haben Norman Cook, Paolo Di Sia und Valerio Dallacasa den Versuch unternommen, den möglicherweise magnetischen Ursprung der starken Kernkraft zu erklären. Die Bedingung dafür, dass sich die Ladungen im selben Lichtkegel befinden, lässt sich dadurch erfüllen, dass der Elektronenabstand [math]d[/math] ein ganzzahliges Vielfaches der Compton-Wellenlänge ausmacht, während die rotierenden Ladungen sich in derselben Phase der Zitterbewegung bewegen:

[math]d = n \lambda_e[/math]

(8)

Die äußerst restriktiven Bedingungen, unter denen Gleichung 6 zur Anwendung kommen kann, lassen sich nur in sehr speziellen Umgebungen realisieren. In wird eine derartige Vorgehensweise vorgeschlagen, bei der der Spinwert [math]\pm \hbar / 2[/math] als Komponente eines Elektronendrehimpulses [math]\hbar[/math]~ parallel zu einem äußeren Magnetfeld aufgefasst wird, während das Elektron wie ein winziger Kreisel der Larmorpräzession unterworfen ist. Diese ganz spezielle, halbklassische Interpretation des Spins schließt nicht aus, dass der Drehimpuls des Elektrons unter bestimmten Bedingungen auf das äußere Magnetfeld ausgerichtet sein kann, wodurch sich die Elektronen wie Elementarteilchen mit ganzem Spin [math]\hbar[/math]~ verhalten. In diesem Fall können die Elektronencluster sogenannte Bose-Einstein-Kondensate ausbilden, in denen die Phasen der Elektronenzitterbewegung synchronisiert sind und die Elektronenabstände der Gleichung (8) entsprechen. In einer solchen hypothetischen Struktur hoher Ordnung und geringer Entropie wird die Coulomb-Abstoßung in Übereinstimmung mit (6) durch die magnetische Kraft [math]F_L[/math] ausgeglichen. In Abschnitt 2.3 werden wir eine Lagrange für [math]N[/math] wechselwirkende geladene Teilchen vorstellen, die die mögliche Existenz dieser kohärenten Zustände nahelegt.

In wird eine grundlegende Verbindung zwischen den Aharonov-Bohm-Gleichungen und einem Elektronenmodell vorgestellt, wobei von einer geometrischen Interpretation der komplexen Phase der Wellenfunktion des Elektrons ausgegangen wird. Dieser Ansatz legt die Möglichkeit nahe, eine effiziente Erzeugung von Elektronenkondensaten unter Ausnutzung des Aharonov-Bohm-Effekts zu erreichen – einem Phänomen, das die Abhängigkeit der Wellenfunktionsphase des Elektrons von elektromagnetischen Potenzialen zeigt. In wird die Hypothese aufgestellt, der zufolge ein Spannungspuls mit einer sehr kurzen, kritischen Anstiegszeit die Bildung kohärenter und dichter Elektronencluster begünstigen kann: „Die Vermutung beruht auf der Möglichkeit, dass es infolge des Aharonov-Bohm-Effekts zu einer schnellen, kollektiven und gleichzeitigen Veränderung der Zitterbewegungsphase kommt, wodurch die Bildung kohärenter Systeme katalysiert wird“.

2.3. Die Darwin-Lagrange

In seiner Arbeit „Magnetic energy, superconductivity, and dark matter“ unterstreicht Prof. Essén die Bedeutung der magnetischen Fernwechselwirkungen für Systeme, an denen eine große Zahl von geladenen Teilchen beteiligt ist. Als ein mögliches nützliches Instrument zur Modellierung solcher Wechselwirkungen schlägt er eine Darwin-Lagrange [math]L_D[/math] vor, die die elektromagnetischen Potenziale mit der kinetischen Energie in Beziehung setzt:

[math]L_D = \sum\limits^N_{a = 1} \left[ \large\frac{m_a}{2} v^2_a \, - \, \large\frac{e_a}{2} \phi_a (\pmb{r}_a) \, + \, \large\frac{e_a}{2 c} \pmb{v}_a \, \cdot \, \pmb{A}_a \, (\pmb{r}_a) \right][/math],	(9)
[math]\pmb{A}_a \, (\pmb{r}_a) = \sum\limits^N_{b \neq a} \large\frac{e_b \left[ \pmb{v}_b + (\pmb{v}_b \, \cdot \, \pmb{r}_{uab}) \, \pmb{r}_{uab} \right]}{2 c r_{ab}}[/math],
[math]\phi_a \, (\pmb{r}_a) = \sum\limits^N_{b \neq a} \large\frac{e_b}{r_{a b}}[/math]
[math]r_{a b} = | \pmb{r}_a - \pmb{r}_b |[/math]
[math]\pmb{r}_{uab} = \large\frac{\pmb{r}_a - \pmb{r}_b}{| \pmb{r}_a - \pmb{r}_b |}[/math]

In diesen Gleichungen werden die Bezeichnungen [math]a[/math] und [math]b[/math] als Indizes für die geladenen Masseteilchen verwendet, [math]\pmb{r}_a[/math] bezeichnet deren Raumkoordinaten, [math]e_a[/math] deren Ladungswert, [math]\pmb{v}_a[/math] deren Geschwindigkeit und [math]m_a[/math] deren Masse. [math]\pmb{A}_a \, (\pmb{r}_a)[/math] und [math]\phi \, (\pmb{r}_a)[/math] bezeichnen den Vektor bzw. das elektrische Potenzial von [math]\pmb{r}_a[/math], und [math]N[/math] steht für die Gesamtzahl der wechselwirkenden Teilchen. Es kommt das Gaußsche Einheitensystem zur Anwendung.

Die Darwin-Lagrange lässt sich konzeptionell vereinfachen, indem man anerkennt, dass der mechanische Impuls [math]\pmb{p}_a[/math] eines geladenen Massenelementarteilchens einen rein elektromagnetischen Ursprung besitzt:

[math]\pmb{p}_a = m_a \pmb{v}_a = \large\frac{e_a}{c} \pmb{A}_{azp}[/math]

In dieser letzten Gleichung steht [math]\pmb{A}_{azp}[/math] für jene Komponente des Vektorpotenzials [math]\pmb{A}_{az}[/math], welche durch den Zitterbewegungsstrom erzeugt wird und parallel zum Geschwindigkeitsvektor [math]\pmb{v}_a[/math] des Teilchens verläuft. Das ermöglicht es, einen Term der kinetischen Energie zu formulieren, der lediglich aus einer Funktion des magnetischen Vektorpotenzials besteht:

[math]\large\frac{m_a}{2} v^2_a = \large\frac{p^2_a}{2 m_a}[/math]
[math]\large\frac{p^2_a}{2 m_a} = \large\frac{e^2_a A^2_{azp}}{2 c^2 m_a}[/math]
[math]m_a = \large\frac{e_a A_{az}}{c^2}[/math]
[math]\large\frac{p^2_a}{2 m_a} = \large\frac{e_a A^2_{azp}}{2 A_{az}}[/math]

Für nichtrelativistische Geschwindigkeiten kann man schreiben:

[math]\large\frac{A_{azp}}{A_{az}} \simeq \large\frac{v_a}{c}[/math]

(10)

Da es sich bei [math]v_a[/math] und [math]A_{azp}[/math] um parallele Vektoren handelt, lässt sich das Produkt ihrer Module durch das Punktprodukt ersetzen:

[math]\large\frac{m_a}{2} v^2_a = \large\frac{e_a v_a A_{azp}}{2 c} = \large\frac{e_a}{2 c} \pmb{v}_a \cdot \pmb{A}_{azp}[/math]

(11)

Somit lassen sich die Terme der kinetischen Energie in die Terme des Vektorpotenzials einbetten:

[math]\pmb{A}_{a t} \, (\pmb{r}_a) = \pmb{A}_{azp} + \pmb{A}_a \, (\pmb{r}_a)[/math]	(12)
[math]L_D = \sum\limits^N_{a = 1} \left[ - \large\frac{e_a}{2} \phi_a \, (\pmb{r}_a) + \large\frac{e_a}{2 c} \pmb{v}_a \cdot \pmb{A}_{a t} \, (\pmb{r}_a) \right][/math]	(13)

Gleichung 13 stellt eine Neufassung von Gleichung 9 dar, wodurch deutlich wird, dass die elektromagnetischen Potenziale eine grundlegendere Rolle spielen, wenn man berücksichtigt, dass alle Terme der kinetischen Energie sich als Funktion des magnetischen Vektorpotenzials darstellen lassen.

2.4. Die Zitterbewegung-Lagrange

Die Komponente [math]\pmb{A}_{azp}[/math] in Gleichung 12 steht bei nichtrelativistischen Geschwindigkeiten nur für einen winzigen Bruchteil des durch die Zitterbewegung erzeugten Vektorpotenzials [math]\pmb{A}_{az}[/math], so wie dies in Gleichung 10 aufgezeigt wird. Diese Feststellung legt die Möglichkeit nahe, eine neue Lagrange zu schreiben, die die Rolle von [math]\pmb{A}_{az}[/math] nicht außer Acht lässt.

Geht man für die Elektronen von einem geeigneten, rein elektromagnetischen Modell der Zitterbewegung aus, dann besteht der erste Schritt auf diesem Weg darin, das Konzept der „geladenen Masseteilchen“ durch die grundlegendere Idee der masselosen Elementarladungen [math]e[/math] zu ersetzen, welche sich mit Lichtgeschwindigkeit und mit einem mechanischen Impuls fortbewegen, dessen Wert proportional zum Punktprodukt aus deren Geschwindigkeit und dem Vektorpotenzial ausfällt. Diese Variante impliziert die Möglichkeit, dass das Vektorpotenzial, das mit der Energie der Ruhemasse verbunden ist, bei den magnetischen Wechselwirkungen eine aktive Rolle spielt. Wechselwirkungen bestehen nur zwischen jenen Ladungen, die sich im selben Lichtkegel befinden. Das hat zur Folge, dass es sich bei ihrem Abstand zueinander innerhalb der Minkowski-Raumzeit um einen lichtartigen (nilpotenten) Vektor handeln muss (siehe hierzu Gleichung 23). Bei Verwendung natürlicher Einheiten, für die [math]\hbar = c = 1[/math] gilt, besitzt diese Lagrange der relativistischen Wechselwirkung eine sehr einfache Form:

[math]L_z = \sum\limits^N_{a = 1} \left[ e_a \pmb{c}_a \cdot \pmb{A}_a \, (\pmb{r}_a) - e_a \phi_a \, (\pmb{r}_a) \right][/math]

(14)

Um die Gültigkeit von Gleichung 14 zu bestätigen, muss nachgewiesen werden, dass sie die klassische Lagrangesche Definition erfüllt:

[math]L = T - U[/math]	(15)
[math]T = \sum\limits^N_{a = 1} e_a \pmb{c}_a \cdot \pmb{A}_a \, (\pmb{r}_a)[/math]
[math]U = \sum\limits^N_{a = 1} e_a \phi_a \, (\pmb{r}_a)[/math]

Gemäß den Ehrenberg-Siday-Aharonov-Bohm-Gleichungen bestimmt sich die geometrische Phase der Zitterbewegung nach dem Vektorpotenzial (Gleichung 16) und nach dem elektrischen Potenzial (Gleichung 17):

[math]d \varphi_{a M} = e_a \pmb{A}_a \, (\pmb{r}_a) \cdot d \pmb{l}[/math]
[math]d \pmb{l} = \pmb{c}_a d t[/math]
[math]d \varphi_{a M} = e_a \pmb{A}_a \, (\pmb{r}_a) \cdot \pmb{c}_a d t[/math]	(16)
[math]d \varphi_{a E} = e_a \phi_a \, (\pmb{r}_a) \, d t[/math]	(17)

Dividiert man die Gleichung 16 durch [math]d t[/math], erhält man den Wert der Zitterbewegungsfrequenz der Ladung [math]e_a[/math] – einen Wert, der dem der relativistischen Massenenergie des Teilchens [math]a[/math] entspricht:

[math]\omega_{\! zbw} = \large\frac{d \varphi_{a M}}{d t} = m_a[/math]
[math]T = \sum\limits^N_{a = 1} m_a[/math]

Diese Feststellungen bestätigen, dass Gleichung 14 die klassische Definition einer Lagrange erfüllt, zumal die „kinetische Energie“ der masselosen Elektronenladung exakt ihrer relativistischen Masse entspricht.

Das Vektorpotenzial [math]\pmb{A}_a \, (\pmb{r}_a)[/math] ergibt sich aus der Summe des Selbstwechselwirkungsterms [math]\large\tfrac{e_a c_a}{\alpha r_{e a}}[/math] und einem weiteren Wechselwirkungsterm:

[math]\pmb{A}_a \, (r_a) = \large\frac{e_a \pmb{c}_a}{\alpha r_{e a}} + \sum\limits_{b \neq a} \large\frac{e_b [\pmb{c}_b + (\pmb{c}_b \cdot \pmb{r}_{uab}) \, \pmb{r}_{uab}]}{r_{a b}}[/math]	(18)
[math]\phi_a \, (\pmb{r}_a) = \large\frac{e_a}{\alpha r_{e a}} + \sum\limits_{b \neq a} \large\frac{e_b}{r_{a b}}[/math]	(19)
[math]L_z = \sum\limits^N_{a = 1} \left\{ \large\frac{1}{r_{e a}} + \sum\limits_{b \neq a} \large\frac{\alpha \pmb{c}_a \cdot \pmb{c}_b + \alpha (\pmb{c}_b \cdot \pmb{r}_{uab})(\pmb{c}_a \cdot \pmb{r}_{uab})}{r_{a b}} - \large\left[ \frac{1}{r_{e a}} + \sum\limits_{b \neq a} \large\frac{\alpha}{r_{ab}} \right] \right\}[/math]	(20)
[math]L_z = \sum\limits^N_{a = 1} \sum\limits_{b \neq a} \large\frac{\alpha [\pmb{c}_a \cdot \pmb{c}_b + (\pmb{c}_b \cdot \pmb{r}_{uab})(\pmb{c}_a \cdot \pmb{r}_{uab}) - 1]}{r_{ab}}[/math]	(21)
[math]\pmb{r}_{a b} = \pmb{r}_a - \pmb{r}_b[/math]
[math]r_{a b} = | \pmb{r}_a - \pmb{r}_b |[/math]
[math]\pmb{r}_{uab} = \large\frac{\pmb{r}_{a b}}{r_{a b}}[/math]
[math]\pmb{c}_a \cdot \pmb{c}_b = cos (\vartheta_{a b 1})[/math]
[math]\pmb{c}_a \cdot \pmb{r}_{uab} = cos (\vartheta_{a b 2})[/math]
[math]\pmb{c}_b \cdot \pmb{r}_{uab} = cos (\vartheta_{a b 3})[/math]
[math]\vartheta_{a b 1} = \vartheta_{a b 2} - \vartheta_{a b 3}[/math]
[math]L_z = \sum\limits^N_{a = 1} \sum\limits_{b \neq a} \large\frac{\alpha \, [cos(\vartheta_{a b 2} - \vartheta_{a b 3}) + cos(\vartheta_{a b 2}) \, cos(\vartheta_{a b 3}) - 1]}{r_{a b}}[/math]
[math]L_{z a b} = \large\frac{\alpha \, [cos(\vartheta_{a b 2} - \vartheta_{a b 3}) + cos(\vartheta_{a b 2}) \, cos(\vartheta_{a b 3}) - 1]}{r_{a b}}[/math]

In den zuletzt aufgeführten Gleichungen bezeichnet [math]r_a[/math] die allgemeine räumliche Position der masselosen Ladung [math]e_a[/math], [math]\pmb{c}_a[/math] deren Einheitsgeschwindigkeitsvektor [math]\pmb{c}^2_a = 1[/math], [math]\alpha = e^2_a[/math] die Feinstrukturkonstante [math]\alpha^{-1} \approx 137\,036[/math], [math]r_{e a}[/math] den Zitterbewegungsradius, [math]r_{a b}[/math] den euklidischen Abstand zwischen den masselosen Ladungen und [math]t_{a b}[/math] ihren zeitlichen Abstand. [math]\pmb{r}_{uab}[/math] ist ein Einheitsvektor, der die gleiche Richtung aufweist wie [math]\pmb{r}_{ab}[/math]. Der Kehrwert des Zitterbewegungsradius in natürlichen Einheiten ist gleich dem Wert der relativistischen Masse des geladenen Teilchens ([math]m_{e a} = r^{-1}_{e a}[/math]). Das Produkt [math]\alpha r_{e a}[/math] ergibt den Ladungsradius.

Die Phasenraumtrajektorie der [math]N[/math] Ladungen wird durch die stationäre Aktionsbedingung [math]\delta \, (\mathscr{S}) = 0[/math] bestimmt.

[math]\mathscr{S} = \int\limits_{\triangle T} L_z \, d t[/math]

Nach Gleichung 21 weist die Vorgehensweise die folgende einfache Form auf:

[math]\mathscr{S} = \sum\limits^N_{a = 1} \sum\limits_{b \neq a} \int\limits_{\triangle T} \large\frac{\alpha \, [cos(\vartheta_{a b 2} - \vartheta_{a b 3}) + cos(\vartheta_{a b 2}) \, cos(\vartheta_{a b 3}) - 1]}{r_{a b}} \, dt[/math]	(22)
[math]\mathscr{S} = \sum\limits^N_{a = 1} \sum\limits_{b \neq a} \int\limits_{\triangle T} \, L_{zab} \, dt[/math]
[math]\delta \, (L_{z a b}) = 0 \Longrightarrow \delta \, (\mathscr{S}) = 0[/math]
[math]\delta \, (L_{z a b}(r_{a b}, \vartheta_{a b 2}, \vartheta_{a b 3})) = \large\frac{\partial L_z}{\partial r_{a b}} \delta r_{a b} + \large\frac{\partial L_z}{\partial \vartheta_{a b 2}} \delta \vartheta_{a b 2} + \large\frac{\partial L_z}{\partial \vartheta_{a b 3}} \delta \vartheta_{a b 3} = 0[/math]
[math]\large\frac{\partial L_z}{\partial r_{a b}} = - \large\frac{\alpha \, [cos(\vartheta_{a b 2} - \vartheta_{a b 3}) + cos(\vartheta_{a b 2}) \, cos(\vartheta_{a b 3}) - 1]}{r^2_{a b}}[/math]
[math]\large\frac{\partial L_z}{\partial \vartheta_{a b 2}} = \large\frac{\alpha \, [-sin(\vartheta_{a b 2} - \vartheta_{a b 3}) - sin(\vartheta_{a b 2}) \, cos(\vartheta_{a b 3})]}{r_{a b}}[/math]
[math]\large\frac{\partial L_z}{\partial \vartheta_{a b 3}} = \large\frac{\alpha \, [sin(\vartheta_{a b 2} - \vartheta_{a b 3}) - cos(\vartheta_{a b 2}) \, sin(\vartheta_{a b 3})]}{r_{a b}}[/math]
[math]r^2_{a b} - c^2 t^2_{a b} = 0[/math]	(23)

Aus diesen Gleichungen lässt sich ablesen, dass die Kohärenzbedingung (Gleichung 24) das Prinzip der stationären Wirkung erfüllt:

[math](\vartheta_{a b 1} = 2 \pi n) \cap \left(\vartheta_{a b 2} = \large\frac{\pi}{2} + \pi m\right) \Longrightarrow \delta \, (\mathscr{S}) = 0 \hspace{1.5em} (n, m \in \mathbb{Z})[/math]

(24)

Sind diese Kohärenzbedingungen erfüllt, gleicht die Lorentzkraft die Coulomb-Abstoßung aus, so wie bereits in Abschnitt 2.2. aufgezeigt. Dies würde auch die hohe Dichte an Elektronenclustern erklären, wie sie von Kenneth Shoulders untersucht wurde.

2.5. Die Entropie von kohärenten Clustern

Obwohl sich bei den Ladungsclustern die Bildung von kohärenten Zuständen mit der Voraussetzung einer stationären Aktion (Gleichung 22) durchaus verträgt, schränkt die extrem niedrige Entropie solcher Zustände deren Wahrscheinlichkeit jedoch stark ein. Die Größenordnung des Verhältnisses der Entropie nichtkohärenter zu der kohärenter Konfigurationen entspricht in etwa der Anzahl [math]N[/math] von wechselwirkenden Elementarteilchen – vorausgesetzt, dass sich der kohärente Zustand durch eine einzige „Wellenfunktion“ beschreiben lässt, so wie dies auch für das Bose-Einstein-Kondensat (BEK) der Fall ist.

Die Darwin-Lagrange lässt sich auf nichtkohärente Zustände von [math]N[/math] wechselwirkenden Elektronen anwenden, die über Zeiträume beobachtet werden, deren Dauer größer ist als die einer Zitterbewegung ([math]t_z \simeq 8,1 \cdot 10^{-21} \, s[/math]). Unter diesen Umständen entfällt der Durchschnittswert der orthogonal zur Elektronengeschwindigkeit verlaufenden Vektorpotentialkomponente und spielt für die magnetischen Wechselwirkungen keine Rolle. Vielmehr verbirgt dieser sich im Term der kinetischen Energie, welcher den Wert seiner Komponente mit der Elementarladung multipliziert, die der Ruhemasse des Elektrons in natürlichen Einheiten entspricht.

3. Die kohärenten Cluster und die EEDF

Die Winkelfrequenz der Zitterbewegung [math]\omega_{zbw}[/math] entspricht exakt der relativistischen Massenenergie [math]m[/math] von Elektronen in natürlichen Einheiten:

[math]\omega_{zbw} = m[/math]

Die relativistische Massenenergie [math]m[/math] entspricht dabei der Summe aus der Ruhemasse [math]m_0[/math] und der kinetischen Energie [math]E_k[/math].

[math]m = m_0 + E_k[/math]

Die kollektive Phasenverriegelung in den Ladungsclustern erfordert „monochromatische Elektronen“ oder eine sehr enge Verteilung der Zitterbewegungsfrequenz und folglich kann durch eine Umgebung mit einer schmalbandigen Elektronenenergieverteilungsfunktion (EEDF) die Bildung solcher kohärenten Strukturen begünstigt werden. Die EEDF stellt in der Plasmaentladung eines Gasgemisches eine Funktion des Druckes und der Gaszusammensetzung dar, so dass durch eine geeignete Einstellung dieser die EEDF verengenden Parameter die Bildung solcher Aggregate begünstigt werden kann.

4. Die Energie aus dem Vakuum

In seinem Buch „An Introduction To A Realistic Quantum Physics“ definiert Giuliano Preparata das Vakuum als „die Schablone der physikalischen Realität“, die „der Schöpfung nicht vorausgeht, sondern vielmehr einen grundlegenden Bestandteil von ihr darstellt“.

Diesem Standpunkt folgend vertreten einige Autoren die Ansicht, dass der Schlüssel zum Verständnis der Entstehung von Materie und Energie aus dem Vakuum im magnetischen Vektorpotential sowie im Aharonov-Bohm-Effekt liegt, womit sie die weithin akzeptierte Auffassung, nach der das Vektorpotential lediglich ein nützliches mathematisches Werkzeug darstellt, völlig umkehren. In ihrer Arbeit „Aharonov-Bohm effect as the basis of electromagnetic energy inherent in the vacuum“ leiten die Autoren ausgehend von diesem Konzept ab, dass „es im Prinzip möglich ist, Geräte herzustellen, die im Sinne des Aharonov-Bohm-Effekts aus dem Vakuum eine unbegrenzte Menge an elektromagnetischer Energie entnehmen, ohne dabei das Noether-Theorem zu verletzen“.

Innerhalb dieses konzeptionellen Rahmens ist Puthoff der Überlegung nachgegangen, dass es prinzipiell möglich ist, durch die Nutzung des Vakuumdrucks aus der elektromagnetischen Nullpunktsstrahlung sowohl Energie als auch Wärme zu gewinnen. Ein Verfahren, mit dem dieses Ziel erreicht werden könnte, wurde in dem US-Patent US7379286 vorgestellt, in welchem die Autoren die Möglichkeit einer lokalen Energieextraktion in Betracht ziehen, die „sich an jedem beliebigen Ort aus dem und durch das elektromagnetische Quantenvakuum wieder auffüllt“.

Die Idee, dass das Vakuum eine Struktur besitzt und dazu genutzt werden kann, um der Umgebung Energie zu entziehen, erfordert eine klare Definition dieser Struktur sowie von deren Verhältnis zu Energie und Materie. Der erste Schritt besteht also darin, die elektromagnetischen Potenziale als „Vakuumstruktur“ zu begreifen und folglich als die grundlegenden Einheiten der physikalischen Realität anzuerkennen. Der zweite Schritt erfordert eine Kodierung dieser Beziehungen sowohl hinsichtlich der Energiedichte als auch des Energieflusses im Raum-Zeit-Kontinuum. Wenn wir mit [math]\square[/math] den Vierergradienten und mit [math]\gamma_t[/math] den Einheitsvektor entlang der Zeitachse der Minkowski-Raumzeit bezeichnen, lässt sich ein Skalarfeld [math]\mathcal{S}[/math] definieren, das die Viererdivergenz des elektromagnetischen Viererpotentials [math]\mathscr{A}[/math] ist:

[math]\mathscr{A} = \pmb{A} + \gamma_t \phi[/math]
[math]\square \cdot \mathscr{A} = \mathcal{S}[/math]

Die Ableitungen des Viererpotentials können nun als ein Operator betrachtet werden, der den Einheitsvektor [math]\gamma_t[/math] in den vier Dimensionen der Raumzeit „rotiert“, wodurch ein Vierervektor entsteht, dessen Zeitkomponente der Vakuumenergiedichte [math]U[/math] entspricht sowie die drei Raumkomponenten dem Flussvektor der Energiedichte [math]\pmb{P}[/math]:

[math]\large\frac{1}{8 \pi} \left(\square \mathscr{A} \gamma_t \, \widetilde{\square \mathscr{A}} \right) = U \gamma_t + \pmb{P}[/math]
[math]\pmb{P} = - \large\frac{1}{4 \pi} \, (\pmb{E} \times \pmb{B} - \mathcal{S} \pmb{E})[/math]	(25)

Wie zu erkennen ist, handelt es sich bei dem Vektor [math]\pmb{P}[/math] um die Summe zweier anderer Vektoren: beim ersten handelt es sich um den Poynting-Vektor, während der zweite Vektor dem Produkt aus dem Skalarfeld [math]\mathcal{S}[/math] und dem elektrischen Feld [math]\pmb{E}[/math] entspricht. Als Folge der weit verbreiteten Nutzung der Lorenz-Eichung ([math]\square \cdot \mathscr{A} = 0[/math]) werden das Skalarfeld [math]S[/math] und der Vektor [math]\mathcal{S} \pmb{E}[/math] von der etablierten Fachliteratur im Allgemeinen ignoriert, obwohl ihre Bedeutung bereits von zahlreichen Autoren hervorgehoben wurde .

Kombiniert man nun das Gaußsche Gesetz (Gleichung 26) mit der Komponente [math]{S E}/{4 \pi}[/math] des verallgemeinerten Poynting-Vektors [math]\pmb{P}[/math], so ergibt sich für die Energiestromdichte eine Nicht-Null-Divergenz, welche ganz eindeutig auf das Vorliegen einer Energiequelle oder einer Energiesenke schließen lässt, bei der weder die Ladungsdichte [math]\rho[/math] noch das Skalarfeld [math]\mathcal{S} [/math] verschwinden. Im vorliegenden Fall entspricht die Ableitung nach der Zeit der Energiedichte [math]U[/math] dem Produkt aus der Ladungsdichte [math]\rho[/math] und dem Skalarfeld [math]\mathcal{S}[/math].

[math]4 \pi \rho = \nabla \cdot \pmb{E}[/math]	(26)
[math]\rho \mathcal{S} = \large\frac{1}{4 \pi} \nabla \cdot \pmb{E} S[/math]
[math]\large\frac{d U}{d t} = \rho \mathcal{S}[/math]	(27)

Diese Ableitung der Energiedichte nach der Zeit lässt sich als Leistungsfluss interpretieren, wie er sich aus einer Ableitung des elektrischen Potenzials [math]\phi[/math] ergibt, welche nicht null ist:

[math]\large\frac{d U}{d t} = \rho \large\frac{d \phi}{d t}[/math]

Integriert man über ein Volumen, das ein einzelnes Elektron einschließt, so wird aus Gleichung 27:

[math]e S = e \large\frac{d \phi}{d t}[/math]

(28)

Kombiniert man nun Gleichung 28 mit der Differentialform der elektrischen Aharonov-Bohm-Gleichung (Gleichung 29), so erkennt man, dass das Vorhandensein eines skalaren Feldes zu einer Veränderung [math]\delta \omega_{zbw}[/math] der Zitterbewegungsfrequenz des Elektrons [math]\omega_{zbw}[/math] und zum Auftreten einer Kraft [math]\pmb{f}_S[/math] führt:

[math]e \phi = \large\frac{d \varphi}{d t}[/math]	(29)
[math]\delta \omega_{zbw} = \large\frac{d \varphi}{d t}[/math]
[math]e \mathcal{S} = \large\frac{d e \phi}{d t}[/math]
[math]e \mathcal{S} = \large\frac{d^2 \varphi}{d t^2}[/math]
[math]e \mathcal{S} = \large\frac{d \omega_{zbw}}{d t}[/math]	(30)
[math]\phi = \int\limits{\mathcal{S} d t}[/math]	(31)
[math]\pmb{f}_S = - e \nabla \phi[/math]

Experimentelle Daten deuten darauf hin, dass ein intensiver Impulsstrom von radialer/zylindrischer Symmetrie und mit einer kritischen Anstiegszeit ein Skalarfeld erzeugt, welches wiederum radiale Kräfte hervorruft, die die Ladungen einschließen und damit die Voraussetzungen dafür schaffen, dass es zur Bildung der in den vorhergehenden Abschnitten beschriebenen kohärenten Aggregate kommt. Diese radiale Ladungsverschiebung kann durch eine geeignete Elektrodengeometrie bewirkt werden oder auch durch einen Stauchungseffekt mittels kurzer und intensiver Stromimpulse. Gleichung 30 beschreibt eine Änderung der Massenenergie, deren Vorzeichen vom dem des Produktes [math]e \mathcal{S}[/math] abhängt: Dieser Prozess ist die Folge einer Vakuumpolarisation, die durch das Vorhandensein des Skalarfeldes [math]\mathcal{S}[/math] verursacht wird: Dies impliziert die Möglichkeit einer Wechselwirkung von großer Reichweite, die in einem Masse-Energie-Transfer von positiv geladenen Teilchen zu negativ geladenen Teilchen oder umgekehrt besteht. Dieser Transfer von Masse verstößt offensichtlich nicht gegen den Energieerhaltungssatz und führt offensichtlich auch nicht zur Instabilität der Kerne der im Plasma vorhandenen positiven Ionen, auch wenn von einigen Autoren die Möglichkeit behauptet wird, dass Skalarfelder die Kerndynamik verändern können. Die winzige Menge an Energie, die die Kerne verlieren, kann durch deren Wechselwirkung mit dem aktiven Vakuum wieder ausgeglichen werden.

Die Hypothese, nach der ein Mechanismus des Massentransfers die Ursache für die anomale Wärmeentwicklung im E-Cat-QX sein könnte, wurde bereits in einem früheren Beitrag vorgestellt, allerdings innerhalb anderer theoretischer Rahmenbedingungen.

Um die in einem Gerät wie dem E-Cat-QX erzeugte Leistung bewerten zu können, muss davon ausgegangen werden, dass die thermische Energie durch den Übergang der Elektronen von einem kohärenten in einen inkohärenten Zustand erzeugt wird, bei dem der Abstand der Elektronen im kohärenten Zustand gleich der Compton-Wellenlänge der Elektronen ist ([math]\lambda_e \approx 2,43 \cdot 10^{-12} \; m[/math]):

[math]I = 0,25 \; A[/math]
[math]\large\frac{d n _e}{d t} = \large\frac{I}{e} = 1,56 \cdot 10^{18} \; n_e / s[/math]
[math]E_e = \large\frac{1}{4 \pi \varepsilon_0} \large\frac{e^2}{\lambda_e}[/math]
[math]\omega_{out} = E_e \large\frac{d n_e}{d t} \simeq 150 \omega[/math]

5. Neutrale pikometrische Aggregate

In einer pikometrischen Größenordnung ([math]10^{-12} \, m[/math]), die zwischen der atomaren ([math]10^{-10} \, m[/math]) und der nuklearen Skala ([math]10^{-15} \, m[/math]) liegt, können sich bei Anwesenheit von Protonen kompakte neutrale Aggregate bilden, die aus einer kohärenten Kette bosonischer Elektronen bestehen, bei denen sich die Protonen im Zentrum der Orbits von deren Zitterbewegung befinden. Eine wichtige Voraussetzung für die Entstehung derartiger Strukturen bildet dabei eine kritische, von der Kathodentemperatur abhängige Schwelle der Elektronendichte.

Die Existenz von Elektron-Proton- und Elektron-Deuteron-Strukturen dieser Größenordnung wurde bereits experimentell nachgewiesen und untersucht. In anerkennt Holmlid die Zitterbewegung des Elektrons als die zugrundeliegende Erklärung für solche Aggregate: „Diese Elektronenspinbewegung kann als eine Bewegung interpretiert werden, bei der sich die Ladung mit dem Bahnradius [math]r_q = {^\hbar\!/_{\! 2 m_e}} \, c \approx 0,192 \; pm[/math] und mit der Lichtgeschwindigkeit [math]c[/math] bewegt (`zitterbewegung')“. Wichtig ist anzumerken, dass dieser Wert für den Radius, wie er von Holmlid, Maruani und Hestenes vorgeschlagen wird, die Hälfte des Wertes des zbw-Radius [math]r_e[/math] beträgt, wie er in angegeben ist, und dass die Wahl eines solchen Wertes ([math]r_q = r_e / 2[/math]) impliziert, dass zwischen dem „intrinsischen“ Drehimpuls des Elektrons und dem Spin keine Unterscheidung getroffen wird, was somit die Möglichkeit der Existenz von „bosonischen Elektronen“ mit [math]spin = \hbar[/math] ausschließt.

Ein interessanter Aspekt der in beschriebenen Elektron-Proton-Wechselwirkungen besteht in der Möglichkeit, die Existenz einiger spezifischer Spektralsignaturen experimentell überprüfen zu können. Nach kann die Elektronenladung ein Proton in einem Abstand von etwa [math]r_e = 0,38 \; pm[/math] umkreisen. Die intensive magnetische Flussdichte [math]B_{zbw}[/math], wie sie durch die rotierende Ladung im Zentrum der Stromschleife der Zitterbewegung erzeugt wird, beträgt

[math]B_{zbw} = 32,21 \cdot 10^6 T[/math] .

Damit beträgt das gyromagnetische Protonenverhältnis [math]g_H[/math]

[math]g_H = 267,52 \cdot 10^6 \, rad \cdot s^{-1} \cdot T^{-1}[/math]

und folglich beträgt der Wert für die kernmagnetische Resonanz

[math]\nu_{N M R} = \large\frac{g_H \, B_{z b w}}{2 \pi} = 1,3714 \cdot 10^{15} \; Hz[/math]

und die relative Präzessionsfrequenz [math]\nu_p[/math] beträgt

[math]\nu_p = \nu_{NMR} / 2 = 6,8571 \cdot 10^{14} \; Hz[/math] .

Diese Frequenz entspricht im Spektrum des sichtbaren Lichtes einer Wellenlänge von

[math]\lambda_p = \large\frac{c}{\nu_p} = 4,372 \cdot 10^{-7} \; m[/math] .

Das Vorhandensein dieser Linie im Spektrum des E-Cat-Plasmas liefert einen möglichen Hinweis auf die Existenz dieser Art von pikometrischen Aggregaten. Ein stärkerer und zuverlässigerer Hinweis in diese Richtung ergibt sich aus der Beobachtung, dass es sich bei der Amplitude dieser Spektrallinie um eine eindeutige Funktion des im Plasma vorhandenen Wasserstoffisotops handelt: Die Linie erscheint deutlich abgeschwächt, wenn anstelle von Protium für die Ladung Deuterium verwendet wird. Diese Feststellung wird durch die Beobachtung gestützt, dass ein Deuteron ein viel kleineres gyromagnetisches Verhältnis aufweist als ein Proton ([math]g_D = 41,066 \cdot 10^6 \; rad \cdot s^{-1} \cdot T^{-1}[/math]). In Anbetracht der starken chemischen Ähnlichkeit von Deuterium und Protium verrät dieser große makroskopische Unterschied in der Spektralemission unter gleichen Bedingungen seinen nuklearen Ursprung.

6. Der Versuchsaufbau

Die Plausibilität dieser Hypothesen wird durch eine Reihe von Experimenten gestützt, die mit dem E-cat SK durchgeführt wurden. Der E-cat SK wurde so aufgestellt, dass das Objektiv eines Spektrometers dessen Plasma in einem dunklen Raum exakt erfassen kann: Ein Ohmmeter misst den Widerstand des Stromkreises, welcher den E-cat mit Energie versorgt; die Steuerungskonsole ist an eine 220-V-Steckdose angeschlossen, während von dieser Konsole die beiden mit den Plasmaelektroden verbundenen Kabel ausgehen. Für zusätzliche Messungen wurden mit dem Plasma ein Frequenzmesser, ein Laser und ein Teslameter verbunden. Darüber hinaus kam zur Untersuchung der elektrischen Ladung des Plasmas ein Van-de-Graaff-Elektronenbeschleuniger (200 kV) zum Einsatz. Bei weiteren Instrumenten des Versuchsaufbaus handelt es sich um einen Spannungsgenerator/Modulator, zwei Oszilloskope (eines für die Stromquelle und eines zur Überwachung der vom E-Cat verbrauchten Energie), Omega-Thermoelemente zur Messung des [math]\Delta T[/math] der Kühlluft, ein IR-Thermometer, einen Frequenzgenerator, einen Geigerzähler und Blasensäulen zur Messung der Emissionen ionisierender Strahlung und von Neutronen.

7. Die Leistungsbewertung des E-Cat SK

In den folgenden Berechnungen wird die Leistung des E-Cat SK zusammengefasst. Die Plasmatemperatur lässt sich mit Hilfe der Wien-Gleichung berechnen. Mit [math]b[/math] als der Konstante des Wienschen Verschiebungsgesetzes und mit [math]\lambda_{max}[/math] als der beobachteten Spitzenwellenlänge der Strahlung ergibt sich

[math]T_k = \large\frac{b}{\lambda_{max}}[/math]
[math]T_k = \large\frac{2,898 \, \cdot \, 10^{-3}}{0,3575 \, \cdot \, 10^{-6}} = 8106 \; K[/math] .

Unter Verwendung des Stefan-Boltzmann-Gesetzes lassen sich die Leistungsabgabe sowie die durchschnittliche pro Stunde erzeugte Energie berechnen:

[math]W_{out} = \sigma \varepsilon T^4_k A \approx 22 \; kW[/math]
[math]E_{out} = 22 \; kWh[/math]

worin [math]\sigma = 5,67 \cdot 10^{-8} \; W m^{-2} K^{-4}[/math], [math]\varepsilon = 0,9[/math] (unter Annahme eines nicht perfekten Schwarzkörpers) und [math]A \approx 10^{-4} \; m^2[/math] (die Länge des zylinderförmigen Plasmakerns beträgt [math]l \approx 1 \; cm[/math], während sein Durchmesser [math]d \approx 0,3 \; cm[/math] beträgt).

Da das Spektrum der Strahlung keine vollständige Maxwellsche Kurve aufweist, muss dieser Wert mit den kalorimetrischen Messungen abgeglichen werden. Der E-Cat wurde in einem Labor eines Industrieunternehmens im US-Bundesstaat Tennessee installiert, um dort einen Raum mit einer Grundfläche von ca. 300 m² und einer Höhe von ca. 5 m warmzuhalten. Zum Zeitpunkt der Messungen betrug die Außentemperatur etwa 0 °C (32 °F) und die Temperatur im Raum etwa 16 °C (61 °F). Um diese Temperatur aufrechtzuerhalten, wurde zuvor ein Heizgerät mit einer Leistung von etwa 20 bis 22 kW betrieben.

Die Einzelheiten:

Durchsatz des Gebläses: [math]5500 \; m^3 / h \simeq 6700 \; kg / h[/math]

[math]\Delta T = 16 \, ° \! C[/math]

[math]C_p \; air = 0,17[/math]

[math]W = 6700 \times 0,17 \times 16 = 18224 \; kcal/h = 20,5 \; kWh/h[/math]

Es wurde auch ein Test mit einem Luftstrom von [math]330 \; m^3/h[/math] durchgeführt und dabei ein [math]\Delta T \; von \; 312 \; ° \! C[/math] erreicht.

Bei kontinuierlichem Betrieb produziert der E-Cat SK innerhalb von 60 Tagen 30 000 kWh an Wärme, was einem Äquivalent von etwa 2600 kg Heizöl entspricht, und er vermeidet damit gleichzeitig die Emission von mehr als 8000 kg CO₂. Nehmen wir nun als Beispiel die Energie [math]E_{inp}[/math], die das Steuergerät innerhalb einer Stunde verbraucht

[math]E_{inp} = 380 \; Wh[/math]

dann lässt sich die durchschnittliche Leistungszahl (COP) als das Verhältnis von Ausgangs- und Eingangsenergie berechnen:

[math]COP = \large\frac{E_{out}}{E_{inp}} \approx 54[/math]

Fazit

In diesem Beitrag wurden drei verschiedene, sich nicht gegenseitig ausschließende Ansätze für die Wechselwirkung von Teilchen mit großer Reichweite im E-Cat SK vorgestellt. Der erste basiert auf der möglichen Rolle der Casimir-Kraft in dichten Elektronenaggregaten: zwei verschiedene Ansätze, von denen einer auf Zitterbewegung-Elektronenmodellen basiert, deuten beide darauf hin, dass die Coulomb-Abstoßung zwischen Elektronen auf einer pikometrischen Skala ausgeglichen werden kann. Der zweite, in Analogie zur Idee von Norman Cook über den magnetischen Ursprung der starken Kraft, befasst sich mit den Lorentzkräften in kohärenten Systemen, in denen die Zitterbewegungsphasen der Elektronen synchronisiert sind und die Elektronenladungen sich im selben Lichtkegel befinden. Es wurde eine relativistische Wechselwirkungslagrange für eine Gruppe von geladenen Elementarteilchen vorgestellt, die die mögliche Existenz dieser kohärenten Zustände nahelegt. Es wurde die Hypothese aufgestellt, nach der besondere Entladungsgeometrien und -dynamiken zur Entstehung einer Vakuumpolarisation führen, welche die Bildung dieser entropiearmen Strukturen begünstigt. Die dritte Hypothese basiert auf dem möglichen elektrostatischen Abschirmeffekt, wie er bei virtuellen Teilchenpaaren durch die Fluktuationen des Quantenvakuums hervorgerufen wird.

Als Folge dieser relativ weitreichenden Wechselwirkungen wurde die mögliche Bildung von dichten Aggregaten im Pikometermaßstab angenommen. Es wurde über eine isotopenabhängige spektrale Signatur des E-Cat-Plasmas im sichtbaren Bereich einer pikometrischen Proton-Elektron-Struktur berichtet.

Danksagung

Ich bedanke mich bei Carl Oscar Gullström und Giorgio Vassallo für die interessanten Diskussionen und die Zusammenarbeit an diesem Thema.