Condensed Plasmoids – The Nuclear Active Environment in LENR (ICCF22)

22nd International Conference on Condensed Matter Nuclear Science (ICCF22)
8. bis 13. September 2019, Assisi in Italien
Lutz Jaitner:
Condensed Plasmoids – The Nuclear Active Environment in LENR

Kondensierte Plasmoide – Die nuklearaktive Umgebung von LENR

Video
Lutz Jaitner im Vortrag
Plattform	youtube.com
Kanal	Assisi Nel Vento
URL	youtube.com/watch?v=Gl9paQbjywk
Datum	29.09.2019
Länge	35 Minuten, 8 Sekunden

Die LENR-Forschung beschäftigte sich schon seit geraumer Zeit mit den grundlegenden Fragen: Wie können Atomkerne bei niedriger Temperatur fusionieren? Warum wird die beobachtete Überschusswärme nicht von Gammastrahlung begleitet? Warum wird bei LENR das Helium-4 aus Deuterium erzeugt, während bei der Heißen Fusion hauptsächlich Helium-3, Tritium und Neutronen entstehen? Wie kann LENR in technischer Hinsicht für die kommerzielle Nutzung optimiert werden?

Zur Beantwortung dieser Fragen hat der Autor ein quantenmechanisches Modell für die nuklearaktive Umgebung von LENR entwickelt. Diese Umgebung besteht aus einem ultradichten Plasmoid, genauer gesagt, einem „Kondensierten Plasmoid“ (Condensed Plasmoid - CP). Die berechneten Eigenschaften der CPs sind derart exotisch, dass CPs als ein bislang unbekannter Aggregatzustand der Materie eingestuft werden können.

Das quantenmechanische Modell von CPs basiert auf der zylindrischen Symmetrie eines sehr dünnen (etwa 40 pm) Plasma-„Drahtes“ (die in der Zusammenfassung angegebenen quantitativen Eigenschaften hängen von der Konfiguration des CPs ab, stellen aber lediglich Beispiele dar). Die Elektronen eines CP sind vollständig delokalisiert und von den Atomkernen entkoppelt. Sie bewegen sich gegenüber den Atomkernen mit sehr hoher Geschwindigkeit (10 bis 80 Prozent der Lichtgeschwindigkeit). Dies führt in den CPs zu einem intrinsischen Strom von etwa 9 kA, bei einer mittleren Stromdichte von etwa 2,5 A pro Quadratpikometer.

Das von diesem Strom verursachte Magnetfeld erreicht eine Stärke von 50 Megatesla und erzeugt einen Einschlussdruck von mehr als 10²¹ Pa (Zettapascal). Die Elektronen werden durch den Zustand des z-Pinch auf eine mittlere Dichte von etwa 0,15 Elektronen pro Quadratpikometer komprimiert.

Die Erzeugung von CPs stellt einen endothermen Prozess dar, der in der Regel hohe Spannungen und hohe Stromstärken erfordert. Sobald sie erzeugt worden sind, besitzen die CPs eine Lebensdauer, die sich über Stunden erstrecken kann. Diese Langlebigkeit ist wahrscheinlich nicht auf die Stabilität der CP selbst zurückzuführen, sondern beruht vielmehr auf einer selbsterhaltenden Rückkopplung von Kernenergie, die dem ansonsten unvermeidlichen Zerfall der CP entgegenwirkt.

Der Mindestabstand zwischen den Wasserstoffkernen in einem CP beträgt gerade einmal 2 pm, was das Tunneln durch die Coulombbarriere ermöglicht. Darüber hinaus wird die Barriere in hohem Maße auch durch die dichten Elektronen abgeschirmt.

Sollte die Reaktionsrate über die Brennstoffmenge nicht angemessen begrenzt werden, kann das selbsterhaltende Wachstum von CPs zu einer gefährlichen und schlagartigen Freisetzung von Kernenergie führen.

Hallo allerseits. Mein Name ist Lutz Jaitner. Ich komme aus Deutschland.

Ich bin seit 2006 auf diesem Gebiet tätig. Ich möchte mich bei Ihnen für die Einladung bedanken, hier einen Vortrag zu halten.

Ich hatte mich für das Rätsel namens LENR interessiert. Und ich wollte es lösen, was mich dann doch über einen langen Zeitraum beschäftigt hat. Mein Ziel bestand darin, eine Lösung dafür zu finden, LENR mit den etablierten Prinzipien der Physik in Einklang zu bringen. Und dies hat sich als ein schwieriger Weg erwiesen. Aber ich denke, dass ich etwas herausgefunden habe, was in dieses Bild passt.

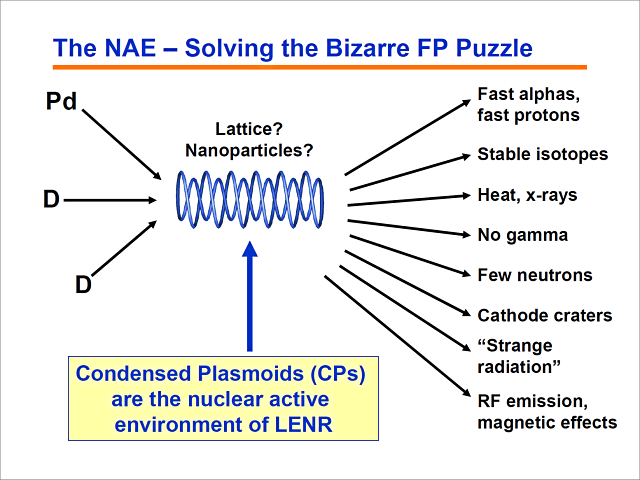
Das Rätsel, wie es sich mir stellte, bestand demnach aus einigen Eingangselementen, die zu einer bestimmten Reaktion führten und Ergebnisse lieferten, die im Widerspruch zu den etablierten Prinzipien der Physik zu stehen schienen.

Wie hier bereits dargelegt wurde, kam es zu einer Beobachtung von Helium, das aus Alphateilchen hervorgegangen sein könnte. Dabei wurden einige Protonen emittiert, jedoch nicht viele. Es kommt zur Bildung von stabilen Elementen anstelle von radioaktiven Isotopen. So gesehen bestand insbesondere in der Abwesenheit von Tritium ein Puzzlestück, das nicht so recht passen wollte. Es wird Wärme abgegeben und es kommt zu Röntgenstrahlung – nicht aber zu Gammastrahlung. Es wurden kaum Neutronen nachgewiesen. Die Kathode zeigte manchmal sehr interessante Krater, die sich nicht so einfach erklären ließen.

Und in letzter Zeit häufen sich die Beobachtungen einer merkwürdigen Strahlung. Ich werde später noch darauf zurückkommen. Ich werde erklären, worum es sich dabei handelt bzw. was wir bei den Experimenten beobachtet haben. Und auch das war etwas, was nicht ins traditionelle Bild passen wollte. Darüber hinaus kommt es zu einigen hochfrequenten Emissionen und zu einigen sehr interessanten magnetischen Effekten.

All dies führt somit zu einem Rätsel, das ich unbedingt lösen wollte. Ich habe mir die aktuellen Erklärungen angesehen, die in der Gemeinde dazu vorliegen. Und ich habe mich dann gefragt: Könnte es am Gitter liegen? Erscheint es plausibel, dass das Gitter zu einer solchen Reaktion führt? Daraufhin habe ich Unmengen an Dokumenten analysiert, welche von den Experimentatoren bereits verfasst worden waren. Und ich konnte darin keine überzeugenden Beweise dafür finden, dass sich die Reaktion tatsächlich im Gitter vollzieht. Denn dann müssten im Gitter ja die Reaktionsprodukte erscheinen. Und ich konnte auch keinen Beweis dafür ausfindig machen, dass eine Vergrößerung der Materialoberfläche zu einer proportionalen Erhöhung der Reaktionsgeschwindigkeit führen würde.

Also habe ich den Versuch unternommen, irgendetwas anderes als den Zwischenzustand oder die kernaktive Umgebung von LENR einzuführen, und ich habe es Kondensierte Plasmoide genannt – daher auch der Titel dieser Präsentation. In meinen Ansätzen geht es also darum, mit Hilfe der Quantenmechanik einen Zwischenzustand zu berechnen, der über eine wesentlich höhere Elektronendichte verfügt als normale Materie, um so die Reaktion erklären zu können.

Lassen Sie uns also über diese merkwürdige Strahlung sprechen. Ich bin der Meinung, dass es sich bei dieser merkwürdigen Strahlung um dasselbe handelt, nämlich um Kondensierte Plasmoide. Was man also in einigen der Experimente zu sehen bekommt, ist exakt dieser Zwischenzustand.

Die merkwürdige Strahlung oder auch die Kondensierten Plasmoide wurden schon sehr oft gesichtet und von Experimentalphysikern wie Winston Bostick mit den unterschiedlichsten Namen versehen. Er nannte sie Wirbelfilamente innerhalb unserer Stromfilamente. Auch Ken Shoulders hatte sie beobachtet und gab ihnen den Namen EVs oder EVOs. Dann war da noch Takaaki Matsumoto. Er nannte sie Ringcluster oder so ähnlich. Und es gab Beobachtungen durch Savvatimova und Rodinov. Es gab Beobachtungen durch Urutskoev. Ich glaube, er bezeichnete sie als merkwürdige Strahlung. Von ihm habe ich diese Bezeichnung übernommen. Und dann waren da noch die aktuelleren Fotografien von Claude Daviau und seinen Mitarbeitern.

Es sind auch andere Bezeichnungen gebräuchlich, wie zum Beispiel Mikrokugelblitze und dergleichen. Das Phänomen wurde also über einen ziemlich langen Zeitraum beobachtet, doch niemand konnte erklären, worum es sich dabei handelt.

Schauen wir uns also an, in welcher Form sie in den Experimenten in Erscheinung treten, was dort zu beobachten ist. Eines der ersten Fotos der LENR-Forschung stammt von Mosier-Boss und ihren Mitarbeitern bei der SPAWAR. Dabei handelt es sich offenbar um kleine Krater, die wie geschmolzenes Palladium auf einer ansonsten nicht geschmolzenen Oberfläche aussehen. Man bezeichnete sie als Mikroexplosionen, weil man davon ausging, dass für dieses Schmelzen wohl eine sehr große Menge an Wärmeenergie verantwortlich gewesen sein muss. Ich denke nicht, dass es sich hierbei um ein Schmelzen handelt, ich denke auch nicht, dass es sich um einen thermischen Effekt handelt – aber was zu erkennen ist, ist ein Krater. Andere Experimentatoren haben andere Krater gesehen. Ken Shoulders zum Beispiel war in der Lage, mit sehr wenig Energie kleine Objekte zu erzeugen, die auf Oberflächen trafen und dabei Krater verursachten, die ebenfalls wie geschmolzen aussahen. Dann waren da noch Elektrolyseexperimente vom Typ der Fleischmann-Pons-Elektrolyse. Dabei wurde eine Art Krater erzeugt, der zwar nicht geschmolzen, aber doch interessant genug war und sich mit den anderen Bildern vergleichen lässt.

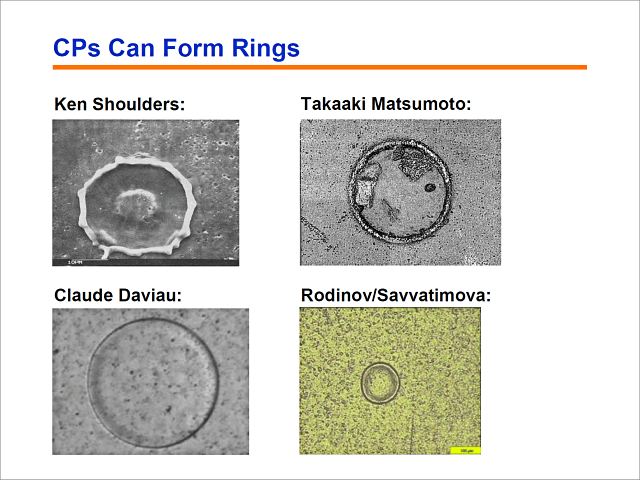
Es sind auch verschiedene andere Formen dieses Objektes anzutreffen. Sie sehen also nicht immer gleich aus. Ken Shoulders fand diese Ringstruktur auf einem seiner Targets, was ihn sehr neugierig auf die Natur dieser Objekte werden ließ. Matsumoto sah diese Ringcluster, und zwar sehr viele von ihnen im Rahmen seiner Elektrolyseexperimente. Dann entstand da eine Fotografie eines Röntgenfilms, wohl von Claude Daviau, mit einem sehr klaren Bild mit einem sehr schönen Ring. Ein ähnliches Foto gab es auch von einem Röntgenfilm von Rodinov und Savvatimova. Dies zeigt ein weiteres Beispiel dessen, was möglich ist.

Und seltsamerweise finden sich in einigen Fällen periodische oder quasi-periodische Strukturen ganz unterschiedlicher Art, und dies in vielen Varianten. In meinem Modell, das ich noch erläutern werde, existiert eine Grundstruktur, eine selbstorganisierte Struktur dieser Objekte, die sich dazu nutzen lässt, all diese komplizierten Muster zu beschreiben, wenn man sie nur leicht verändert. Dies deutet somit darauf hin, dass die von mir entwickelte Erklärung und die mikroskopischen Bilder aus diesen Experimenten ein und dasselbe darstellen.

Lassen Sie mich nun erklären, worin der grundlegende Gedanke meiner Theorie besteht, denn ich glaube, dass man diesen sehr einfach verstehen kann und dass sich ein jeder ein Bild davon machen kann. Diese Gleichung hier gibt die Stärke des Magnetfeldes an der Oberfläche eines stromdurchflossenen Drahtes an. Also nichts Besonderes, nur die übliche Lehrbuchformel. Das Interessante daran ist nun, dass der Radius des Drahtes im Nenner steht, was zur Folge hat, dass es für den Fall, dass der Radius gegen null geht, zu einer Singularität kommt.

Überlegen wir nun, was das bedeutet. Nehmen wir einmal an, dass es sich bei dem Draht nicht um ein Stück Metall handelt, sondern um ein Plasma, ein stromdurchflossenes Plasma, ein Plasmoid. Es handelt sich also um einen Plasmadraht oder eben ein Plasmoid, das diesen Radius aufweist. Gehen wir einmal davon aus.

Was geschieht nun, wenn die Stärke des Magnetfeldes zunimmt? Dann wird es einen Druck auf dieses Plasma ausüben, es entsteht ein Pinch-Effekt, ein sogenannter z-Pinch, wodurch der Draht dünner wird. Die Formel besagt nun, dass bei einem Dünnerwerden des Drahtes auch das Magnetfeld stärker wird, und das führt zu einer Art von positiver Rückkopplung. Sobald nun bei der Stromstärke oder bei der Stärke des Magnetfeldes ein kritischer Wert erreicht wird, bleibt dieser sozusagen auf ewig bestehen. Dadurch kollabiert die Materie zu etwas sehr dichtem.

Die interessante Frage ist nun, welche Dichte erreicht werden kann und wo dies aufhört.

Darauf gibt es nun zwei Antworten. Die erste Antwort besagt, dass die Kompression, welche sich in diesem z-Pinch ereignet, die Temperatur normalerweise auf ein solches Maß ansteigen lässt, dass hierdurch ein thermischer Druck entsteht, der bestimmte Instabilitäten verursacht oder dem weiteren Kollaps der Materie ein Ende setzt. Allerdings tritt auch Strahlung aus, insbesondere elektromagnetische Strahlung, die das Plasma abkühlt. Und wenn es sich um einen sehr dünnen Plasmadraht handelt, ist die Kühlung sehr effektiv.

Gehen wir also davon aus, dass die Temperatur niedrig ist und keinen Gegendruck erzeugt. Was wird in diesem Fall passieren, was wird den Kollaps aufhalten? Die Antwort findet sich in dem Entartungsdruck des Elektronengases, einem quantenmechanischen Effekt. Die Elektronen lassen sich nicht auf ein unendlich kleines Volumen komprimieren, da dies zu einer Erhöhung ihrer kinetischen Energie führen würde.

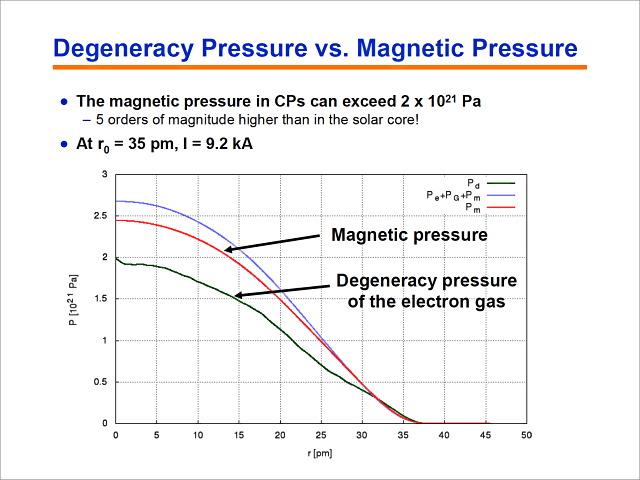
Das ist es, was ich berechnen wollte – die Quantengrenze jener Kompression, wie sie sich im Rahmen eines z-Pinchs einstellt.

Hier nun das Ergebnis einer Plausibilitätsprüfung. Ich wollte sicherstellen, dass meine Berechnungsergebnisse sich in Übereinstimmung mit den in der Physik geltenden Grundformeln befinden. Also habe ich eine in der Astrophysik gängige Formel herangezogen, um den Entartungsdruck in Weißen Zwergen zu berechnen, durch den der Kollaps zu einem Neutronenstern verhindert wird. Dies hier ist also die entsprechende Kurve. Anhand meiner Simulationsergebnisse habe ich den magnetischen Druck berechnet, und sie lagen nicht weit auseinander. Es sieht so aus, als hätte ich es tatsächlich irgendwie hinbekommen, die richtigen Drücke und Kräfte zu berechnen.

Erstaunlicherweise liegt der Druck, der hier ermittelt wurde, bei 2 × 10²¹ Pascal (Zetapascal)). Das liegt 5 Größenordnungen über dem Druck, wie er im Sonnenkern herrscht. Wir sprechen hier also von etwas sehr Exotischem. Es handelt sich hier lediglich um einen z-Pinch, der bis an die Quantengrenze zu etwas anderem kollabiert. Die Ergebnisse, wie sie hier von diesen Kurven dargestellt werden, wurden bei einem Radius von 35 Pikometern und einem Eigenstrom des Drahtes von 9,2 Kiloampere erzielt.

Stellen wir uns nun die Frage, welche Physik für diese Objekte zum Tragen kommt. Für die Beschreibung dieser Objekte können wir uns entweder für die Plasmaphysik entscheiden, da es sich um ein Plasma oder ein Plasmoid handelt. Oder wir entscheiden uns für die Quantenmechanik, was gut wäre, da wir uns mit dem Kollaps auf die Quantengrenze zubewegen.

Schauen wir mal, was das bedeutet. Wenn wir die Plasmaphysik bei niedrigen Temperaturen und hohen Dichten zugrunde legen, was ist dann die Folge? Die Plasmaphysik würde vorhersagen, dass sich die Plasmoide in Atome und Moleküle auflösen. Nun, das ergibt bei diesen Dichten keinen Sinn. Die Atome können gar nicht mehr existieren, weil sie viel zu dicht beieinander liegen. Die Elektronen werden delokalisiert. Es lassen sich also keine Atome mehr feststellen und auch der Stromfluss endet nicht. Das Ganze ist auch bei niedrigen Temperaturen noch leitfähig. Daher würde ich meinen, dass die Plasmaphysik sich nicht in Übereinstimmung mit der beobachteten Lebensdauer dieser Objekte befindet.

Wie die experimentellen Ergebnisse gezeigt hbaen, zerfallen die Plasmoide nicht in normale Atome und Moleküle. Also gelangte ich zu der Überzeugung, dass die Quantenmechanik gebraucht wird. Und um ehrlich zu sein, ich hasse die Quantenmechanik, aber ich war gezwungen, sie zu benutzen. (Richtig?) Und die Quantenmechanik prognostiziert, dass die Kondensierten Plasmoide durch die Delokalisierung der Elektronen im Plasmazustand verbleiben. Einzig dies deckt sich mit der beobachteten Lebensdauer von Kondensierten Plasmoiden, die sich in den Experimenten auf viele Stunden und in einigen Fällen sogar auf einige Tage belaufen hat.

Die nächste Folie veranschaulicht die grundlegenden Annahmen, die ich bei der quantenmechanischen Modellierung zugrunde gelegt habe, um die Eigenschaften zu bestimmen. Ich musste also einige Berechnungen anstellen, und eben für diese Berechnungen benötigte ich ein Modell. Das Modell geht von nur wenigen Annahmen aus. Es geht davon aus, dass es sich um einen langen Kanal handelt, einen Plasmadraht, dessen Atomkerne dicht gepackt sind. Es geht desweiteren davon aus, dass der Abstand zwischen den Kernen so gering ist, dass alle Elektronen entlang dieses Kanals delokalisiert sind. Und die Elektronen bewegen sich relativ zu den Kernen, so dass ein Strom durch diesen Plasmadraht fließt. Das ist schon alles, das ist der ganze Satz von Annahmen – nichts weiter, keine Raketenwissenschaft.

Ich verwende etwas, das hoffentlich schon längst seinen Platz in den Lehrbüchern gefunden hat. Es handelt sich um den Hamiltonian mit einer Art einer sogenannten minimalen Kopplung. Dieser beschreibt die Gesamtenergie eines Elektrons in einem magnetischen Potenzial sowie in einem elektrischen Potenzial. Er sollte also vertraut sein, und man sollte damit zurechtkommen. Bei der Formel handelt es sich um eine relativistische Formel, weil ich die Geschwindigkeit des Elektrons, welche bis zu 80 Prozent der Lichtgeschwindigkeit betragen kann, voraussetze, oder ich werde diese herausfinden. Ich dachte, es wäre genauer, einen relativistischen Hamiltonian zu verwenden.

Wenn man diesen Hamiltonian in eine quantenmechanische Gleichung quantisiert, erhält man die Klein-Gordon-Gleichung, sofern man die Elektronenspins vernachlässigt. Auf diese Weise lässt sich der Hamiltonian auf direktem Wege quantisieren. Ich habe diesen Weg beschritten und zylindrische Koordinaten verwendet, da ich es mit einem langen Plasmadraht zu tun habe. Dieser weist eine zylindrische Symmetrie auf.

Anschließend musste ich das elektrische und das magnetische Potenzial aus den Wellenfunktionen und den Kernladungen berechnen. Dies hier sind die Formeln, die zu diesem Zweck verwendet wurden.

Jetzt musste ich die Klein-Gordon-Gleichung lösen. Und um das zu erreichen, habe ich zunächst einmal diesen Produktansatz aufgestellt. Die Wellenfunktion sollte in etwas zerlegt werden, das in axialer Richtung, in azimutaler Richtung und in radialer Richtung verläuft. Die axiale Wellenfunktionslösung ist bekannt, so dass ich sie hier angeben kann. Das war es dann auch schon. Die azimutale Wellenfunktion ist ebenfalls bekannt. Fertig. Lediglich die Radiowellenfunktion sieht ein wenig komplizierter aus. Hier geht es um die Lösung dieser Komponente der Klein-Gordon-Gleichung, die noch zu lösen ist. Und leider findet sich in der Literatur für diese Differentialgleichung keine analytische Lösung.

Also habe ich folgendes getan: Ich habe einen Ansatz aufgestellt, bei dem die Wellenfunktion approximiert wird. Dies hier ist die radiale Wellenfunktion. Sie wurde durch ein Polynom approximiert, multipliziert mit einer radial abklingenden Exponentialfunktion. Auch die Potenziale und meine Gleichung wurden durch ein Polynom approximiert. Wenn ich dies hier in meine Differentialgleichung einsetze, bekomme ich keine analytische Lösung. Wenn ich dagegen für das Polynom diese Koeffizienten einsetze, bekomme ich eine analytische Lösung, was angenehm ist, da es die Rechenzeit verkürzt.

An dieser Stelle muss ich noch etwas hinzufügen. Und zwar geht es um diese Gleichung hier: (Siehe weiter oben die Folie „Klein-Gordon Equation of a CP“)

Diese geht davon aus, dass ich für ein einzelnes Elektron eine Wellenfunktion mit angemessener Genauigkeit nutzen kann, welche sich aus dem mittleren Potential aller anderen Elektronen sowie der Kerne berechnet. Es handelt sich also wiederum um eine Näherung. Es handelt sich nicht um eine vollständige quantenmechanische Lösung, wie man sie gewöhnlich verwendet. Aber ich habe es schließlich mit Milliarden von Elektronen zu tun. Da muss in meinem Ansatz alles etwas einfacher gehalten werden.

Was ist also bei dieser Simulation herausgekommen? Ich habe ein Programm geschrieben. Ich habe Tausende von Orbitalen simuliert. Und jedes dieser Orbitale repräsentiert Gruppen von großen Gruppen von Elektronen.

Die Zusammenfassung der Parameter, die ich berechnet habe, zeigt, dass es für diese Objekte keine Obergrenze gibt. Sie können wachsen und eine endliche Größe erreichen. Ich habe so etwas wie eine Mindestlänge ermittelt. Die Mindestlänge dieser Objekte bewegt sich in einer Größenordnung von 10 Mikrometern. Das ist keine genaue Angabe, es ist sozusagen nur eine Vermutung.

In der Elektronenverteilung kann ich bei diesen Plasmadrähten einen Radius zwischen 35 und 130 Picometern erkennen. Es handelt sich hierbei um einen Bereich, denn die Kondensierten Plasmoide können in den verschiedensten Konfigurationen existieren.

Die Metadichte in diesen Objekten kann bis zum Hunderttausendfachen der Dichte betragen, die gewöhnliche Materie aufweist. Das unterscheidet sich ganz erheblich von dem, was man bei Experimenten mit Gittern festgestellt hat. – Es handelt sich also um Materie mit einer viel höheren Dichte.

In diesen Objekten fließt ein intrinsischer Strom. Der Strom kann nicht aufhören zu fließen. Wenn der Strom zum Stillstand kommt, verschwindet die Kraft, die den Kanal zusammenpresst, und das ganze Ding explodiert. Es gibt Gründe dafür, dass diese Ströme, nachdem sie einmal durch äußere Bedingungen in Gang gesetzt wurden, immer weiter fließen. Die mittlere Geschwindigkeit der Elektronen liegt zwischen sechzehn und vierzig Prozent der Lichtgeschwindigkeit.

Und die Spannung im Kern dieser Objekte liegt zwischen minus 7 und minus 60 Kilovolt. Der Grund hierfür liegt darin, dass es dort einen Überschuss an negativer Ladung gibt. Das heißt, es gibt in diesen Objekten vielleicht bis zu 2 % mehr Elektronen als Kernladungen, wodurch sie Ionen gegenüber eine anziehende Wirkung haben. Die Ionen sind darin sicher eingefangen, die Elektronen aber nicht. Diese könnten einfach davonfliegen, und nur das Magnetfeld hält sie noch am Kern fest.

Ich wollte natürlich auch wissen, wie hoch die Bindungsenergie ist, und das hat sich als eine einzige Enttäuschung erwiesen. Die Bindungsenergie weist einen Wert auf, der zwischen zehn und hundertzwanzig Kiloelektronenvolt pro Elektron beträgt. Es handelt sich also um eine endotherme Bindungsenergie. Aus energetischer Sicht entspricht dies einem ungebundenen Elektron. Ungebunden ist es aber nicht in dem Sinne, dass es davonfliegt, sondern in dem Sinne, dass es dann davonfliegt, wenn die Bewegung der Elektronen gestoppt wird.

Ich betrachte dies also als ein vorläufiges Ergebnis. Ich glaube, dass in meinem Hamiltonian noch einige Terme fehlen, die im Zuge einer späteren Korrektur noch zum Tragen kommen werden. Ich kann es Ihnen im Moment noch nicht sagen, da ich es noch nicht weiß.

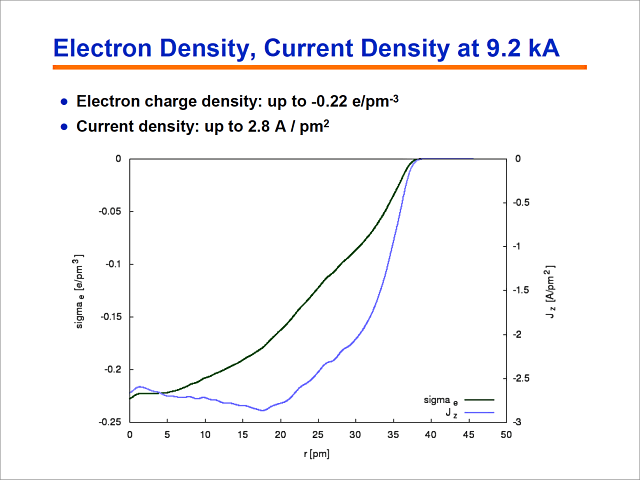
Schauen wir uns die Verteilung der Elektronendichte an. Sie sehen hier also diese beiden Kurven. Die eine stellt die Elektronendichte dar und die andere die Stromdichte.

Wir haben hier eine Elektronendichte von 0,2 Elektronen pro kubischem Picometer, was eine extrem hohe Elektronendichte darstellt.

Wir haben Stromdichten von bis zu 2,8 Ampere pro Quadratpikometer. Das entspricht astronomisch hohen Dichten.

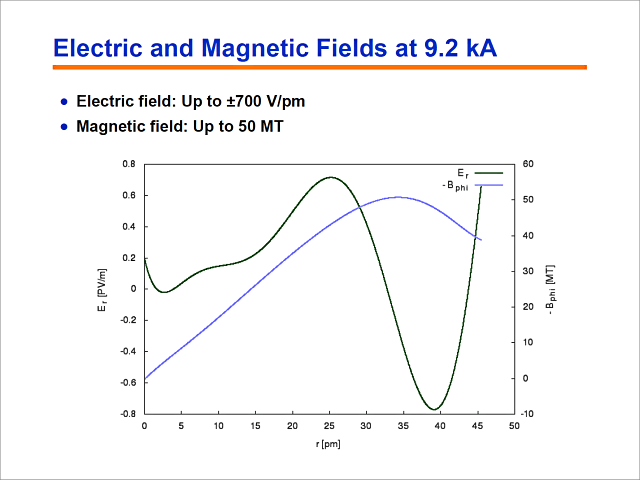
Hieraus lässt sich das elektrische Feld berechnen, das bis zu +/- 700 Volt pro Picometer beträgt.

Es existieren Magnetfelder, deren Stärke bis zu 50 Megatesla beträgt. Das ist vergleichbar mit dem Magnetfeld eines Pulsars – dem astronomischen Objekt Pulsar. Das sind Werte, die sich so im Labor auf mikroskopischer Ebene nicht erzielen lassen. Aber im mikroskopischen Maßstab handelt es sich sehrwohl um derart extreme Felder.

Wenn Sie dieses Ergebnis der Simulation akzeptieren können, dann stellt sich Ihnen doch sicher die Frage: Welche Möglichkeiten ergeben sich daraus? In welchem Zusammenhang steht dieses Ergebnis mit den LENR-Experimenten?

Ein entscheidender Faktor bei der Umsetzung dieser Ergebnisse in experimentelle Ergebnisse besteht in dem Mindestabstand zwischen den Kernen, wie er sich aus den Berechnungen ergibt, und der beträgt beispielsweise bei Wasserstoff zwei Picometer, bei Sauerstoff vier und bei Gadolinium acht.

Dieser Abstand ist meiner Meinung nach klein genug, um das Tunneln durch die Coulombbarriere zu ermöglichen. Die hohe Elektronendichte schirmt die Coulombbarriere zudem noch zusätzlich ab. Die Wahrscheinlichkeit eines Coulombtunnels ist also viel größer.

Und das funktioniert auch mit anderen Elementen, wie hier bei Gadolinium, einem relativ großen Atom. Wie Sie feststellen können, liegt es immer noch so eng beieinander, dass ein Tunneln möglich ist. Wir würden also nicht nur mit Wasserstoff tunneln, sondern mit allen Arten von Elementen.

Außerdem geht es hier tatsächlich um die Kalte Fusion. Die Elemente benötigen für die Fusion keine kinetische Energie, da es sich um reines Tunneln handelt. Und das Schöne daran ist, dass sie für eine sehr lange Zeit nahe beieinander verweilen. Es steht also genügend Zeit zur Verfügung.

Wenn sich ein solches Tunneln ereignet, kann ein Teil der Energie der angeregten Elemente zu einer Spallation führen. Beschränkt man die Betrachtung also nicht nur auf die Fusion selbst, sondern schließt auch die möglichen Ausgangskanäle mit ein, lässt sich die Fusion-Spaltung als eine mögliche Option betrachten.

Dies stellt lediglich eine Hypothese dar – aber ich denke, sie kann erklären, weshalb beispielsweise Elemente wie Helium, Kalzium und Eisen aus Deuterium und Palladium erzeugt werden können. Das wäre von einem einfachen Fusionsprozess so nicht zu erwarten.

In einer weiteren Hypothese vertrete ich die Ansicht, dass die hohe Elektronendichte auch dazu beitragen kann, die Anregungsenergie der Kerne abzuleiten. Wenn also die Kerne angeregt werden und sie mit ihren elektrischen und magnetischen Dipolen vibrieren oder oszillieren, dann kann diese Energie über die hohe Elektronendichte und die hohe Stromdichte absorbiert werden, und die entstehenden Trends verwandeln sich in geringfügige Änderungen der Elektronengeschwindigkeiten. Somit erfolgt hier ein Prozess der Abwärtskonversion.

In einer weiteren Hypothese gehen wir davon aus, dass die hohe Elektronendichte zu einer Verstärkung des Beta-Plus-Zerfalls führt oder zu einer Verstärkung des Elektroneneinfangs zugunsten des Beta-Plus-Zerfalls, was erklären würde, warum keine Annihilationsstrahlung zu beobachten ist, wie sie von Positronen abgegeben wird.

In Experimenten konnten wir feststellen, dass diese Objekte über einen langen Zeitraum hinweg stabil bleiben. Ich meine, dass es eine nukleare Rückkopplung gibt, welche auf die kinetische Energie der Elektronen gerichtet ist. Ich bin also der Auffassung, dass die Abkühlung der Kerne durch die Elektronen zu einer Geschwindigkeitserhöhung und zu einer Erhöhung der Durchschnittsgeschwindigkeit der Elektronen führt, was das Wachstum dieser Objekte und die Erzeugung von Elektrizität in Richtung der äußeren Elektronen erklären würde. Für mich stellt dies in der Sache eine der interessantesten Spekulationen dar.

Ich möchte Sie bitten, mit diesen Objekten vorsichtig umzugehen. Ich habe in der Vergangenheit schon viele Experimente miterlebt, bei denen die Menschen nicht einmal von der Existenz dieser seltsamen Strahlung Kenntnis hatten. Ich bin der Meinung, dass diese Objekte für den menschlichen Körper eine Gefahr darstellen. Bekanntlich können sie intensive Röntgenstrahlung und ultraviolettes Licht produzieren. Dies ist keine Spekulation, sondern eine erwiesene Tatsache. Beobachter als auch Experimentatoren konnten feststellen, dass sie die dicken Wände von LENR-Geräten durchdringen. Sie treten somit unerwartet aus Ihrem Gerät aus. Sie sind in der Lage, ohne Schwierigkeiten elektronische Bauteile zu zerstören. Sie können jegliche Materie ionisieren, was oft den Anschein von Schmelzen hat. Sie konnten das an den Kratern beobachten, die ich Ihnen gezeigt habe. Ich empfehle Ihnen, und das ist wirklich sehr wichtig: Die Geräte benötigen eine ausreichende Abschirmung. Ich empfehle eine wirksame Abschirmung Ihrer Geräte mit dicken Wänden aus Eisen, bis eine bessere Lösung für dieses Problem zur Verfügung steht.

Ich habe da noch eine Folie. – Nun, eine Warnung stellt kein gutes Ende für eine Präsentation dar.

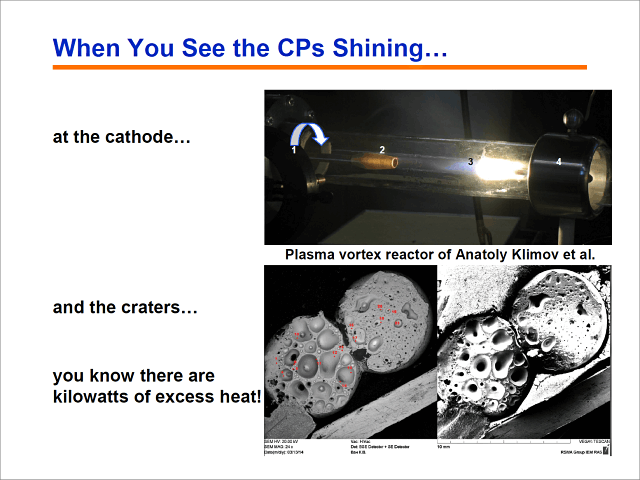
Diese Folie hier zeigt ein Gerät von Anatoly Klimov. Ich danke Ihnen, Anatoly, für dieses ausgezeichnete Experiment. Ich werde hier nicht weiter auf die Details eingehen. Ich werde mich ganz auf die Kathode konzentrieren, die hier eine sehr große Leuchtkraft besitzt. Die Kathoden weisen im Anschluss auf ihrer Oberfläche diese Krater auf.

Die Bemerkung, die ich dazu machen möchte, wäre also, dass sich Kondensierte Plasmoide mit bloßem Auge wahrnehmen lassen, wenn sie über eine hohe Dichte verfügen. Anatoly nennt sie erosive Metallcluster. Das spielt keine Rolle, es ist einfach nur ein anderer Name für ein und dieselbe Sache. Und ich sage Ihnen, wenn Sie diese einmal auf diese Weise glühen sehen und wenn Sie die Krater hier sehen, dann werden Sie keine Kalorimetrie mehr benötigen, um herauszufinden, ob da überschüssige Wärme vorhanden ist. Sie werden einen Wärmeüberschuss im Kilowattbereich verzeichnen.

Die eigentliche Herausforderung besteht nun darin, ein Expertengerät zu entwickeln, wie Anatoly es getan hat, das dieses Glühen hervorbringt. Und damit sind wir schon fast fertig.

Ich danke Ihnen.