Ein neues Verständnis von der Kalten Fusion

The Explanation of Low Energy Nuclear Reaction
A New Understanding of Cold Fusion
Edmund Storms
22. Januar 2024
storms2@ix.netcom.com

Kurzfassung

Es wird eine kurze Beschreibung zu ausgewählten Informationen geliefert, welche derzeit zu dem als Kalte Fusion bezeichneten Fusionsprozess vorliegen und die der allgemeinen Darstellung der vermuteten Funktionsweise dieses Prozesses dienen sollen. Diese Informationen umfassen auch neue experimentelle Ergebnisse aus Studien zur Elektronenemission sowie zur Wirkung des angelegten Elektronenstroms.

Der nukleare Prozess resultiert aus einer ungewöhnlichen chemischen Konstellation, bei der es zur Bildung einer physikalischen Struktur kommt, innerhalb derer sich unzählige Elektronen und einige wenige Wasserstoffkerne zusammenlagern können. Innerhalb dieses Verbundes kann es dann zu einer Kernfusion kommen. Man geht davon aus, dass sich dieser Prozess außerhalb der Gitterstruktur in bestimmten physikalischen Leerstellen von einer kritischen Größe ereignet. Der Fusionsprozess führt zu zwei wesentlichen Ergebnissen. Zum einen verheißt er eine saubere, unerschöpfliche und preiswerte Energiequelle. Zum anderen zeigt sich eine völlig neuartige Form eines nuklearen Prozesses, bei dem sich eine Vielzahl von Elektronen in einer ungewöhnlichen Struktur zusammenfinden. Obwohl der vorgestellte Mechanismus bisher noch nicht in seinen mathematischen Eigenschaften beschrieben werden kann, lassen sich seine wichtigsten Merkmale bereits identifizieren und als Modell für künftige Studien zugrunde legen.

1.0 Einführung

Vor dreiunddreißig Jahren gaben die Professoren Martin Fleischmann und Stanley Pons (F-P) an der University of Utah eine Entdeckung bekannt, die die Wissenschaftsgemeinde in Erstaunen versetzte. Bei ihrer Entdeckung ging es um die Fähigkeit, unter den in gewöhnlichem Palladiummetall befindlichen Deuteriumkernen zu einer Fusionsreaktion zu gelangen, indem man dieses Metall in einer Elektrolytzelle unter Raumtemperatur mit D₂O zur Reaktion brachte. Da diese Entdeckung für die Gesellschaft die Möglichkeit eröffnete, eine sichere, umweltfreundliche und kostengünstige Energiequelle zu erschließen, stieß diese Bekanntgabe weltweit auf großes Interesse. Leider war dieses Interesse nur von kurzer Dauer, weil sich der Mythos verbreitete, dass die beobachteten Reaktionen auf fehlerhaften Messungen beruhten.

In diesem Aufsatz soll daher der Versuch unternommen werden, drei grundlegende Fragen zu beantworten. Erstens: Handelt es sich bei der Kalten Fusion um ein reales Phänomen? Zweitens: Welche Rückschlüsse lassen sich ausgehend vom beobachteten Reaktionsverhalten auf den Reaktionsprozess ziehen? Und drittens: Lässt sich ein logisch widerspruchsfreier Mechanismus ermitteln, welcher in der Lage ist, das beobachtete Verhalten zu erklären, ohne dabei gegen die Gesetze der Naturwissenschaften zu verstoßen? Die Antworten legen den Schluss nahe, dass es sich um eine vollkommen neue Art der Wechselwirkung zwischen Elektronen handeln könnte.

Nach dem konventionellen Verständnis gilt eine derartige Fusionsreaktion als ausgeschlossen, da die zur Überwindung der Coulombbarriere erforderliche Energie nicht vorliegt und die Atomkerne in einem gewöhnlichen Material normalerweise zu weit voneinander entfernt sind, um miteinander in irgendeine Wechselwirkung zu treten. Selbst wenn es zu einer solchen Reaktion käme, wären all jene Reaktionsprodukte zu erwarten, welche im Zuge des konventionellen Mechanismus der Heißen Fusion entstehen. Man hat nach den zu erwartenden Neutronen gesucht, sie aber nicht in der erforderlichen Anzahl gefunden. Darüber hinaus war es den meisten Forschern nicht gelungen, die beschriebene Wärmeerzeugung zu reproduzieren. Diese Probleme führten im Zusammenspiel mit einer Reihe von politischen Faktoren in den USA zu einem Mythos, der sich bis in die Gegenwart fortsetzt. Huizenga erläutert die wissenschaftlichen Gründe für diese Ablehnung, und Krivit beschreibt, auf welche Weise die Ablehnung zustande gekommen ist. Aus den nachfolgend aufgeführten Gründen kann dieser Mythos nicht länger aufrechterhalten werden.

Obwohl das Auslösen eines solchen nuklearen Prozesses aus inzwischen verstandenen Gründen eine Herausforderung darstellt, zeigt sich sein Verhalten, wenn es denn dazu kommt, meist ganz offensichtlich und ohne jeden Zweifel. Das Fehlen einer signifikanten Neutronenemission gilt inzwischen als Charakteristikum der Kalten Fusion, wobei eine gelegentlich festgestellte Neutronenemission durch unterschiedliche Reaktionen hervorgerufen werden kann. Die dabei entstehenden Nuklearprodukte, darunter Tritium (³H) und Helium (⁴He), konnten in zahlreichen unabhängigen Studien identifiziert werden. Das wichtigste Nuklearprodukt stellt im Übrigen die Wärmeenergie dar, wobei die gemessene Energiemenge um viele Größenordnungen über derjenigen liegt, welche sich aus irgendeiner plausiblen chemischen Reaktion ableiten ließe. Diese Wärmeenergie entspricht auch jener Menge an ⁴He, wie sie durch den Fusionsprozess erzeugt wird – wie weiter unten in diesem Artikel noch gezeigt wird.

Für einen Skeptiker mag es vernünftig erscheinen, eine einzelne Messung oder eine ganze Folge von Messungen abzulehnen, sobald sich ein üblicher Fehler herausgestellt hat – allerdings handelt es sich bei einer derartigen Serie von konsistenten Verhaltensmustern, wie sie in zahlreichen unabhängigen Studien nachgewiesen wurden, um jene Art von grundlegenden Beweisen, anhand derer in der Wissenschaft alle Konzepte bewertet werden. Inzwischen liegen Erkenntnisse darüber vor, dass sich verschiedene Verfahren auf den Prozess in einer Weise auswirken, dass ein Fehler oder ein herkömmlicher Prozess als Ursache für dieses Verhalten ausgeschlossen werden kann. Tatsächlich wurden alle seitens der Skeptiker und der etablierten Wissenschaft gestellten Anforderungen erfüllt. Die Herausforderung besteht nun darin zu ergründen, wie der Prozess im Einzelnen vonstatten geht – was das Anliegen des vorliegenden Aufsatzes ist. Dazu gehören auch Vorschläge, auf welche Weise die vorgeschlagene Theorie getestet und in die Praxis umgesetzt werden kann, um auf diesem Wege nutzbare Energie zu gewinnen.

Eine Erklärung wird dadurch erschwert, dass es neben der Kernfusion auch noch zu zahlreichen weiteren Kernreaktionen gekommen ist, welche in verschiedensten Materialien unter Anwendung unterschiedlicher Verfahren hervorgerufen wurden. Dieses unerwartete Verhalten hat dazu geführt, dass der ursprüngliche Begriff der Kalten Fusion durch den von den „Niederenergetischen Kernreaktionen“ (LENR), mitunter auch den der „Nuklearwissenschaft der Kondensierten Materie“ (CMNS) abgelöst wurde. Diese zusätzlichen Reaktionen belegen, dass wir es hier mit einem äußerst komplexen Mechanismus zu tun haben, der einen noch viel größeren Widerspruch zum bisherigen Verständnis aufweist. Diese Abhandlung konzentriert sich jedoch ausschließlich auf die Behauptungen von F-P, wonach bei der Fusion von PdD und anderen Verbindungen, die Wasserstoffisotope enthalten, signifikante Mengen an Energie sowie nukleare Reaktionsprodukte entstehen, wenn sie einem speziellen Verfahren unterzogen werden. Da es sich bei dieser Abhandlung nicht um eine Übersicht handelt, werden für das ausführlich beschriebene Verhalten nur einige wenige Beispiele angeführt. Zusätzliche Informationen finden sich in den zitierten Artikeln. Kopien der zitierten ICCF-Konferenzdokumente, der im JCMNS veröffentlichten Dokumente und viele weitere Dokumente können auf LENR-CANR.ORG heruntergeladen werden. Anstelle einer Bewertung der zahlreichen Konflikte zwischen all den vorgeschlagenen Theorien werden diese Konflikte untersucht, indem solche Fragen gestellt werden, deren Antworten sich aus experimentellen Beobachtungen und nicht aus der Theorie ergeben. Die Antworten wiederum dienen dazu, eine neue Erklärung zu finden, die allein auf dem beobachteten Verhalten basiert. Auch logische Implikationen werden untersucht. Selbst wenn der Versuch unternommen wird, die Zahl der Wunder zu reduzieren, bleibt die Erklärung komplex und erfordert unkonventionelle Denkansätze. Daher empfiehlt sich eine umfassende Lektüre des gesamten Artikels, bevor zu einem Urteil geschritten wird.

Bevor nun die Behauptungen von F-P erörtert werden, sollte der Leser verstanden haben, dass es da zwei unterschiedliche Mechanismen gibt, die in einem Material zu einer Fusion führen können. Der von F-P entdeckte Mechanismus kommt ohne Energiezufuhr aus und wird von daher als Kalte Fusion bezeichnet. Im Gegensatz dazu erfordert der alternative Mechanismus die Zufuhr erheblicher Mengen an zusätzlicher Energie, in aller Regel in Form von kinetischer Energie, welche entweder durch ein Plasma, durch den Einsatz von Laserenergie oder durch Ionenbeschuss zugeführt wird. Deshalb wird dieser Mechanismus auch als Heiße Fusion bezeichnet. Da beide Methoden unterschiedliche Nuklearprodukte in deutlich voneinander abweichenden Raten erzeugen, ist nicht davon auszugehen, dass sie denselben Mechanismus zur Basis haben. In diesem Artikel wird ausschließlich der Mechanismus der Kalten Fusion beschrieben. Für diejenigen unter den Lesern, die das Ergebnis gleich am Anfang der Lektüre erfahren möchten, sind die letztendlichen Schlussfolgerungen dieser Analyse im unten angefügten Anhang I zusammengefasst.

2.0 Das Gesamtverhalten

Der Prozess kann als Folge von vier Phasen betrachtet werden, von denen jede nacheinander als eigenständiges Ereignis abläuft. In den ersten beiden Phasen gelten die Regeln, wie sie normalerweise für chemisches Verhalten zutreffen, da sich die Ereignisse in einer chemischen Umgebung abspielen. Die letzten beiden Phasen unterliegen den Regeln, die für einen nuklearen Prozess gelten. Ein effektives Verständnis davon lässt sich nur dadurch erreichen, dass man die gesamte Abfolge in die Erklärung mit einbezieht. Im Abschnitt 4 werden diese Phasen ausführlicher behandelt. Zunächst müssen jedoch die allgemeinen Merkmale der einzelnen Phasen verstanden werden, da sich dieser Prozess sowohl von jedem herkömmlichen chemischen als auch von jedem nuklearen Vorgang unterscheidet. Wenn man bereits im Voraus versteht, worauf diese Logik hinausläuft, ist es hoffentlich einfacher, dem Weg zu folgen, noch bevor in den nachfolgenden Abschnitten alle Fragen im Detail behandelt werden.

2.1 Chemische Aspekte

Ausgangspunkt bildet die ganz offensichtliche Tatsache, dass sich zur Erzielung einer Kalten Fusion zwei Atomkerne zeitgleich an ein und demselben Ort aufhalten müssen. In einem chemischen System befinden sich die D-Kerne zu weit voneinander entfernt, um eine Wechselwirkung zwischen ihnen zu ermöglichen, denn dieser Abstand wird von der Elektronenstruktur vorgegeben, für die die Regeln der Kristallbildung gelten. Damit es überhaupt zu einer Fusion kommen kann, müssen die Atomkerne und die Elektronen eine gänzlich andere Beziehung zueinander aufbauen, ohne hierbei die Regeln zu verletzen, welche für alle chemischen Systeme gelten. Außerdem würde der chemische Prozess, durch den die Kerne und die Elektronen zusammengebracht werden, im Ergebnis keine Kernreaktion erwarten lassen. Folglich müsste der Prozess, wie alle chemischen Reaktionen auch, den Gesetzen der Thermodynamik folgen, wobei es sich bei der Kernreaktion um ein unvorhersehbares Ereignis handelt.

Als Nächstes muss die Beschaffenheit jener einzigartigen lokalen Bedingungen bestimmt werden, unter denen der Fusionsprozess abläuft, da er sich nicht überall im Material ereignet. Viele der Materialien, in denen sich die Kalte Fusion vollzieht, wie etwa PdD, bestehen aus einer kubisch-flächenzentrierten (fcc) Kristallstruktur, in welcher sich die Atome in einer regelmäßigen Anordnung befinden. Diese Anordnung weist die niedrigste Gibbs-Energie aller möglichen Konfigurationen auf. Eine sehr gute Beschreibung der fcc-Struktur findet sich unter en.wikipedia.org/wiki/Cubic_crystal_system.

Die Kalte Fusion erfordert hingegen die Bildung einer anderen Anordnung. Damit es dazu kommen kann, sollten wir nach solchen Orten Ausschau halten, an denen die chemische Umgebung nicht durch die Regeln einer kristallographischen Anordnung bestimmt wird. Würden die für die Fusion erforderlichen Atome diese Stellen besetzen, dann hätten wir es nicht mehr mit einer fcc-Struktur zu tun – und da alle diese Stellen in chemischer Hinsicht identisch sind, wären sie alle besetzt, sollte auch nur einer von ihnen besetzt werden können. Diese sehr grundlegenden Überlegungen schließen irgendwelche Leerstellen innerhalb der Gitterstruktur als die Stelle für den Fusionsprozess aus.

Damit sich eine die Fusion begünstigende Atomanordnung herausbilden kann, muss darüber hinaus die chemische Stabilität des D in der neuen Anordnung höher sein als an seinem gewöhnlichen Platz innerhalb der Gitterstruktur. Andernfalls würde das D seine Position in der normalen Gitterstruktur nicht aufgeben, um sich der Bildung dieser neuen Struktur zuzuwenden. In Abschnitt 4.2 wird diese Frage ausführlicher behandelt. Wir sind also von Anfang an mit einem einzigartigen chemischen Problem konfrontiert, noch bevor wir überhaupt den Versuch unternommen haben zu verstehen, wie die Fusion selbst zustande kommt.

Da der Fusionsprozess die Herausbildung eines einzigartigen chemischen Zustandes voraussetzt, und da sich derartige Stellen nur sehr selten ausbilden, würde die Gesamtzahl solcher Stellen und die Häufigkeit, mit der sich an jeder dieser Stellen die erforderliche Struktur ausbilden könnte, den Umfang der Energiemenge bestimmen, nicht aber die nukleare Reaktionsrate selbst. Obwohl die Fusionsreaktion eine gewisse Zeit in Anspruch nehmen würde, dürfte zu erwarten sein, dass ihre Rate weitaus höher ist als die des Strukturbildungsprozesses, und zwar sowohl hinsichtlich der initialen Bildung der erforderlichen Struktur als auch hinsichtlich der Ersetzung von D nach seiner Umwandlung in ein anderes Element. Da davon auszugehen ist, dass es der chemische Prozess ist, der die zu beobachtende Energiemenge bestimmt, müssen sich die Bemühungen zur Gewinnung von Nutzenergie auf diesen Aspekt des Prozesses konzentrieren.

2.2 Nukleare Aspekte

Für die Fusion müssen die nuklearen Energiezustände zweier Deuteronen in der Weise miteinander in Wechselwirkung gebracht werden, dass es zu einem neuen Energiezustand kommt, der selbst wieder für ein stabiles Kernprodukt sorgt. Diese Wechselwirkung erfordert eine Herabsetzung der Coulombbarriere, um die Kerne so nahe zusammenzubringen, dass der erforderliche Energieaustausch erfolgen kann. Zur Erreichung dieses Zieles können zwei Verfahren zum Einsatz kommen. Diese beinhalten die Anwendung von kinetischer Energie und/oder die Elektronenabschirmung. Da im Zuge der Kalten Fusion normalerweise zu wenig Energie zur Verfügung steht, um eine brachiale Wechselwirkung zu bewirken, muss sich die Erklärung auf die Elektronenabschirmung konzentrieren. Ein weiterer Mechanismus, das sogenannte Tunneln, kann ebenfalls zur Anwendung kommen, um die offensichtliche Reduzierung der Coulombbarriere herbeizuführen. Beide Ansätze liefern eine Erklärung dafür, auf welchem Wege es zu einer nuklearen Wechselwirkung kommen kann, welche nicht durch die ganze Kraft der Energiebarriere eingeschränkt wird. Auch wenn diese Energiebarriere durch die Elektronenabschirmung herabgesetzt wird, wenn zur Auslösung des Mechanismus der Heißen Fusion der Ionenbeschuss zum Einsatz kommt, fällt das Ausmaß dieser Herabsetzung im Vergleich zum Umfang der Abschirmung, welche zur Auslösung einer Kalten Fusion erforderlich ist, kaum ins Gewicht. Die Herausforderung besteht also darin, eine Lösung für einen stärkeren Abschirmungsprozess zu finden. Vorschläge dazu werden im weiteren Verlauf des Artikels erörtert.

Nachdem sich die Fusion ereignet hat, muss die freigesetzte Kernenergie unter Erhaltung des Impulses abgeführt werden. Dieser Prozess erfordert die Emission von zwei oder mehr nuklearen Reaktionsprodukten. Im Falle der Kalten Fusion wurde lediglich ein Nuklearprodukt als Quelle aller gemessenen Energie identifiziert, nämlich das ⁴He. Dies stellt ein Problem dar, denn ein einzelnes nukleares Produkt ist nicht in der Lage, nukleare Energie unter Erhaltung des Impulses abzugeben. Eine Lösung für dieses Problem wird in Abschnitt 3.8.3 vorgestellt und deren Konsequenzen in Abschnitt 4.3 erörtert.

Der nukleare Prozess kann sich in einer Vielzahl von Materialien vollziehen, und nicht nur im PdD, das ursprünglich zum Einsatz kam. Darüber hinaus sind neben der Elektrolyse mittlerweile zahlreiche weitere Verfahren in der Lage, den Prozess auszulösen, wobei sowohl Deuterium (D) als auch normaler Wasserstoff (H) bei Anwendung geeigneter Materialien ähnliche Mengen an Kernenergie produzieren.

Schließlich muss die freigesetzte Kernenergie abgeführt werden, ohne dabei jedoch eine energiereiche Strahlung zu erzeugen, welche außerhalb des Gerätes nicht nachgewiesen werden kann. Gelegentlich lässt sich eine bestimmte Neutronenemission nachweisen, die allerdings auf Sekundärreaktionen zurückzuführen sein dürfte. Nichtsdestotrotz lassen sich eine bestimmte Menge an Strahlung sowie verschiedene nukleare Reaktionsprodukte nachweisen, vorausgesetzt, innerhalb des Gerätes wird effektiv danach gesucht. Diese Strahlung liefert im Übrigen den Schlüssel zum Verständnis der Komplexität des Prozesses und wird in Abschnitt 3.8 genauer erörtert.

In meinem Buch habe ich einige der zahlreichen vorgeschlagenen Modelle bewertet. In diesem Artikel werde ich diese Bewertung nicht wiederholen. Stattdessen soll hier der stetig wachsenden Liste eine weitere Erörterung hinzugefügt werden. Im vorliegenden Fall stützt sich das Modell lediglich auf das beobachtete Verhalten sowie auf einige begründete Annahmen, ohne dass man sich dabei um die Anwendung von Mathematik oder Quantenmechanik bemüht. Stattdessen werden die Verhaltensmuster identifiziert und eine logische Beziehung zwischen ihnen aufgezeigt. Dieser Ansatz soll deutlich machen, auf welche Weise der nukleare Prozess verstärkt werden könnte, und bietet verschiedene Methoden zur Überprüfung des Modells, indem die vorhergesagten Verhaltensweisen untersucht werden. Es wird eine Herangehensweise empfohlen, die es ermöglicht, den Prozess im Detail zu verstehen, um zukünftige Studien unter Nutzung einer effektiveren Konzeption durchführen zu können. Ein solcher Ansatz ist die Voraussetzung dafür, dass eine zuverlässige mathematische Erklärung gegeben werden kann.

Zusammenfassend lässt sich sagen, dass mit der Kalten Fusion offenbar eine Reihe von chemischen Prozessen verbunden ist, die bei Anwesenheit von Wasserstoffisotopen unvermittelt zu einer Kernreaktion führen können. Bei der Bewertung der hier vorgeschlagenen Erklärung ist in Betracht zu ziehen, dass diese einzigartigen chemischen Zustände möglicherweise weit verbreitet sind, in der Vergangenheit jedoch übersehen wurden, weil sie durch keinerlei nukleares Ereignis offensichtlich geworden waren.

Einen Weg zu finden, um ein Verständnis für dieses Phänomen zu entwickeln und es zur Anwendung zu bringen, ist von großer Bedeutung, da es das Potenzial besitzt, als ideale Quelle für saubere Energie zu dienen, wie sie für das Überleben der Zivilisation auch in der Zukunft benötigt wird.

3.0 Diskussion

Bevor hier nun eine Erklärung abgegeben wird, müssen zunächst zwei Fragen beantwortet werden. Im Einzelnen sind dies: (1) Welche Verhaltensweisen sind für eine Erklärung bedeutsam, und (2) welche Annahmen müssen getroffen werden und wie lassen sich diese begründen? Beschrieben werden nur die wichtigsten Verhaltensweisen sowie ihre Bedeutung für eine Erklärung. Wie Sie feststellen werden, fügt sich jede dieser Verhaltensweisen wie die Teile eines Puzzles zu einem Gesamtbild des Prozesses, das allerdings noch immer unvollständig bleibt. In ihrem Verbund betrachtet, liefern die ausgewählten Verhaltensweisen überwältigende Beweise für die reale Existenz von LENR und zeigen auf, welche Teile des Puzzles noch fehlen. Bei den wichtigen Teilen handelt es sich dabei um die Erzeugung von Energie, die Bildung von nuklearen Reaktionsprodukten und die Emission energiereicher Strahlung, die allesamt in einer logischen Beziehung zueinander stehen, wie weiter unten beschrieben wird. Diese Kombination von Verhaltensweisen belegt, dass die zu beobachtende Energie durch eine Kernreaktion hervorgerufen wird, obgleich es sich dabei um einen äußerst ungewöhnlichen nuklearen Prozess handelt.

3.1 Die Erzeugung von Energie

Das am häufigsten zu beobachtende Merkmal der Kalten Fusion besteht darin, dass mehr Energie erzeugt wird als jedwede plausible chemische Energiequelle liefern könnte. Gemessen wird die Energie in Form von Leistung, ausgedrückt in Watt, mittels Kalorimetern unterschiedlicher Bauart. Die anfängliche Ablehnung beruhte auf der Annahme, dass es bei derartigen Wärmemessungen zu Fehlern kommt. Die Eliminierung der vermuteten Fehlerquellen konnte im Großen und Ganzen durch den Einsatz besserer Kalorimeter sichergestellt werden. In allen Fällen wurden die vermuteten Fehler entweder in nachfolgenden Studien beseitigt oder der Nachweis erbracht, dass sie nicht von Bedeutung sind. Beispiele für diese Fehler und für deren Korrektur sind in meinem Buch beschrieben.

Die Menge an freigesetzter Energie lässt sich durch eine Erhöhung der Temperatur, durch die Anwendung von Laserstrahlen und durch das Durchleiten eines elektrischen Stroms durch das Material steigern. Für die Fusion scheinen alle Wasserstoffisotope geeignet zu sein, wobei dem Deuterium bisher die größte Aufmerksamkeit zuteil wurde. Die Konzentration an Deuterium hat unter bestimmten Bedingungen einen Einfluss auf die Stromerzeugung. Möglicherweise werden in der Zukunft auch noch andere Verfahren an Bedeutung gewinnen.

Die Erzeugung von Energie kann dadurch erreicht werden, dass ein aktives Material unterschiedlichster Art elektrolytischem Strom ausgesetzt wird, dass es einem niederenergetischen Plasma ausgesetzt wird, welches in einem Gas oder in einer Flüssigkeit gebildet wird, dass es mittels Schall oder mechanischer Energie Kavitationen ausgesetzt wird und dass es dem Gas D₂ oder H₂ ausgesetzt wird. Mit anderen Worten: Unabhängig von der Art und Weise, wie der Energieträger an die nuklear aktiven Stellen herangeführt wird und welches Wasserstoffisotop zur Anwendung kommt, zeigt sich immer das gleiche Verhalten. Die entscheidende Größe besteht in der Bildung dieser aktiven Stellen.

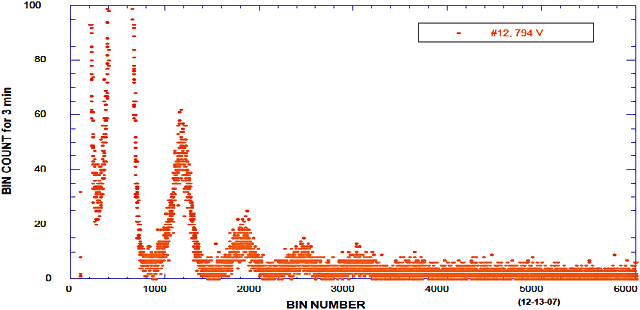
Abbildung 1 enthält ein kleines Beispiel für jene Bemühungen zur Erzeugung von Energie, die zum Erfolg geführt haben. Darin wird die Anzahl an erfassten Werten zu jener Energiemenge in Bezug gesetzt, die bei Raumtemperatur durch PdD-Proben mit vergleichbarer Masse erzeugt wird. Dabei wird deutlich, dass die Zahl der Berichte über erfolgreiche Versuche zur Energieerzeugung mit der Höhe der gemessenen Leistung abnimmt. Bei den meisten Versuchen ist es überhaupt nicht zu einer Energieerzeugung gekommen. Auch wenn dieses Diagramm nur einen sehr kleinen Ausschnitt aus der Gesamtmenge aller derzeit zur Verfügung stehenden Erfolgsberichte wiedergibt, liefert dieses typische Verhalten wichtige Hinweise auf die Natur des Phänomens. Bis einschließlich 2023 wurde in über 500 Veröffentlichungen über die Erzeugung von Überschussenergie berichtet, und dies für zahlreiche unterschiedliche Proben, die alle ein ähnliches Verhalten zeigten.

Abbildung 1: Histogramm, das die Anzahl der erfassten Werte für die bei Raumtemperatur gemessene Leistung zeigt, wie sie von ähnlichen Proben erzeugt wurde, die PdD enthielten und einer Elektrolyse ausgesetzt waren. Die Werte stammen aus Tabelle 2 in „The Science of Low Energy Nuclear Reaction“ aus dem Jahr 2007.

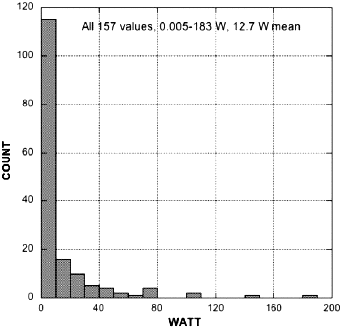
Die Form des Histogramms in Abbildung 1 deutet darauf hin, dass eine Wahrscheinlichkeitsfunktion zum Einsatz kommen könnte, um jene Voraussetzungen zu beschreiben, die für die Verwirklichung des Fusionsprozesses unabdingbar sind. Anders ausgedrückt: Die Kurvenform deutet darauf hin, dass das wahrscheinlichste Ereignis darin besteht, keinen Erfolg zu haben, und dass eine geringe Leistung sehr viel wahrscheinlicher ist als eine große Leistung. Somit kommt der Zufall in der Weise ins Spiel, dass er bestimmt, wie viele einzigartige Stellen in einer bestimmten Probe entstehen werden. Die Herausforderung besteht nun darin, diese Wahrscheinlichkeit der Bildung der erforderlichen Stellen zu erhöhen, um so die Menge der erzielbaren Kernenergie zu steigern. Dabei können wir uns von der Tatsache ermutigen lassen, dass es einige wenige Proben gab, aus denen eine beträchtliche Menge an Energie gewonnen wurde. Diese Zufallserfolge lassen darauf schließen, dass wirksame Methoden zur Steigerung der Leistung existieren müssen, die es jetzt nach und nach zu erschließen und in die Praxis umzusetzen gilt..

3.2 Der Einfluss der Temperatur

Die Temperaturen, mit denen die Energieerzeugung beeinflusst werden soll, sind zu niedrig, um eine direkte Beeinflussung der Kernreaktion zu bewirken. Stattdessen müsste die Temperatur jenen chemischen Prozess beeinflussen, der die nukleare Reaktionsrate begrenzt. Diese Erkenntnis hat der Suche nach diesem begrenzenden Prozess einen Schub verliehen. Bei dieser Suche hat sich ebenso herausgestellt, dass das D/Pd-Verhältnis keinen Einfluss darauf hat, ob es nach dem Einsetzen der Kernreaktion zu einer Erzeugung von Energie kommt.

Die meisten der frühen Studien wurden bei Temperaturen um 20 °C durchgeführt, obwohl F-P festgestellt hatten, dass sich die Leistung durch eine Erhöhung der Temperatur steigern lässt. Sie bezeichneten dies richtigerweise als „positiven Rückkopplungseffekt“, was leider von der Frage abgelenkt hat, auf welche Weise die Temperatur den Prozess beeinflusst. Im Laufe der Jahre haben andere Forscher die Leistung unter verschiedenen Temperaturen gemessen und festgestellt, dass die Leistung mit steigender Temperatur tatsächlich zunimmt. Ich selbst habe mit einem sehr genauen Kalorimeter Messungen über einen breiten Temperaturbereich hinweg durchgeführt und den gleichen Effekt festgestellt, ganz gleich, ob die Messung in der Elektrolysezelle oder in D₂-Gas vorgenommen wurde, so wie in Abbildung 2 dargestellt. Wurde der Strom in der Elektrolysezelle abgeschaltet, was in der Probe zu einem Verlust von D führte, konnte der Temperatureffekt auch nicht durch eine Änderung im resultierenden D/Pd-Verhältnis beeinflusst werden – wie man sehen kann.

Abbildung 2. Wird eine PdD-Probe in einer Elektrolysezelle oder in D₂-Gas erhitzt, ergibt sich die Überschussenergie als eine Funktion der Temperatur. Die Erzeugung von Energie setzte sich bei den höheren Temperaturen fort – auch noch, nachdem der Strom zur Probe in der Elektrolysezelle abgeschaltet wurde. Für die niedrigste Temperatur wurde keine nachweisbare Leistung festgestellt.

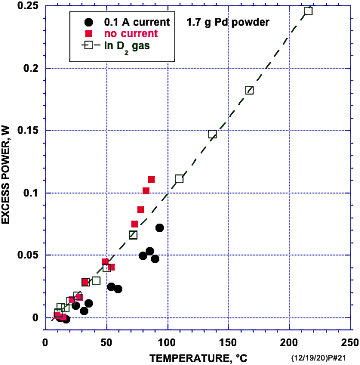
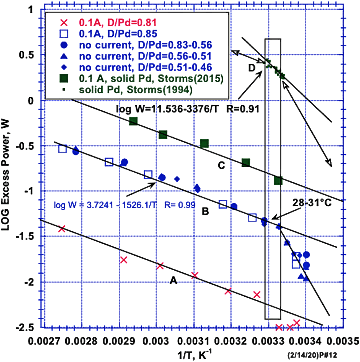
In der Chemie wird die Steigung des Logarithmus der Leistung in Abhängigkeit von 1/T als die Aktivierungsenergie für einen Prozess identifiziert, welcher die Reaktionsrate begrenzt. Dieser Wert gibt die Energiemenge an, die erforderlich ist, um eine Energiebarriere auf dem Weg hin zum Endereignis zu überwinden. In diesem Fall scheint die Aktivierungsenergie für die Wärmeerzeugung mit der Fähigkeit des D oder des H verbunden zu sein, durch chemische Diffusion Zugang zu den nuklear aktiven Stellen zu erhalten, sowohl während der initialen Bildung der Struktur als auch bei der Ersetzung der Wasserstoffkerne, nachdem diese in das nukleare Reaktionsprodukt umgewandelt wurden. Dieser Prozess erfordert, dass die D- oder die H-Kerne von ihren normalen Positionen in der chemischen Struktur wegdiffundieren, um eine Anordnung zu bilden, innerhalb derer der nukleare Prozess erfolgen kann. Ich habe aufgezeigt, dass die Aktivierungsenergie für LENR unter bestimmten Bedingungen der Aktivierungsenergie gleichkommt, welche für die Diffusion von D in PdD benötigt wird, was darauf hindeutet, dass die Erzeugung von Energie unter bestimmten Bedingungen durch die Diffusion des D gesteuert wird. Bei einer Reaktion mit dem D₂-Gas kann sich der Diffusionspfad jedoch recht komplex gestalten. Ein Beispiel für dieses Verhalten ist in Abbildung 3 dargestellt, wo gezeigt wird, dass die Aktivierungsenergie für den in einer Elektrolysezelle stattfindenden Prozess unabhängig ist von der Menge der erzeugten Energie. Sowohl die Aktivierungsenergie als auch die erzeugte Energiemenge sind unabhängig vom D/Pd-Verhältnis, wie in Abbildung 2 zu erkennen ist. Auch hier blieb die Energiemenge nach dem Abschalten des Elektrolysestroms unverändert.

Abbildung 3. Vergleich des Verhaltens verschiedener Proben von massivem und gepresstem Pd-Pulver beim Erhitzen in einer elektrolytischen Zelle. Die Bezeichnungen A, B, C und D stehen für unabhängige Messungen. Die durch die einzelnen Messungen hindurch gezogenen Linien verlaufen parallel, was zeigt, dass sie alle die gleiche Aktivierungsenergie aufweisen. Die mit „D“ bezeichnete Studie lag in einem Übergangstemperaturbereich zwischen zwei unterschiedlichen Werten für die Aktivierungsenergie und wurde in der Legende als „Storms (1994)“ aufgeführt.

Der Zugang der Atomkerne zur aktiven Stelle kann auch dadurch begünstigt werden, dass ein Durchfluss von D-Atomen durch die nuklear aktive Region geschaffen wird, wie von McKubre und anderen dargelegt.

Aus jahrelanger Erfahrung ist bekannt, dass Proben, die bei niedriger Temperatur keine Überschussenergie produzieren, bei Erwärmung häufig doch Energie erzeugen. Vielleicht ist die Kalte Fusion leichter zu erzielen, als es die vielen bei Raumtemperatur scheinbar fehlgeschlagenen Messungen vermuten lassen.

3.3 Der Einfluss des D/Pd-Verhältnisses

Eine Veränderung im D/Pd-Verhältnis hat zahlreiche Auswirkungen, von denen hier nur zwei von Bedeutung aufgeführt werden sollen. Wird das Verhältnis D(H)/Pd erhöht, sinkt die zwischen den D- bzw. den H-Atomen bestehende Bindungsenergie. Dies führt dazu, dass das D bzw. das H in energetischer Hinsicht leichter zur Verfügung stehen, um außerhalb des Kristalls eine weitere Struktur zu bilden, beispielsweise eine Anordnung, wie sie zur Unterstützung des Fusionsprozesses erforderlich ist. Werden darüber hinaus weitere D bzw. H hinzugefügt, dehnt sich der Kristall aus. Diese Ausdehnung kann dann wiederum dazu führen, dass sich um die eingebetteten Teilchen herum Lücken bilden, wie in einem späteren Abschnitt noch beschrieben wird. Bei der Betrachtung der erhöhten Verfügbarkeit von D ist es jedoch wichtig zu berücksichtigen, dass zur Erzeugung einer bestimmten Menge an Energie eine Million Mal weniger D benötigt wird als bei einer entsprechenden chemischen Reaktion. Demzufolge wäre in einer Gitterstruktur nur eine äußerst geringe Menge an D erforderlich, um eine Reaktionsrate zu erreichen, aus der eine beträchtliche Menge an Energie gewonnen werden kann. Wie lässt sich diese Erwartung nun mit dem beobachteten Verhalten in Einklang bringen?

Wie aus Abbildung 4 hervorgeht, konnten McKubre und Kollegen feststellen, dass eine Erhöhung des D/Pd-Verhältnisses zu einem Anstieg der Energiemenge führt, wenn eine spezielle Charge des Pd zum Einsatz kommt. Ein ähnliches Verhalten wurde auch von Kamimura und anderen festgestellt. Allerdings wurde von Storms beschrieben und in dessen Abbildungen 2 und 3 gezeigt, dass nicht immer ein besonders großes D/Pd-Verhältnis erforderlich ist, um eine Energieerzeugung zu erzielen. Wieso einige Proben empfindlich auf das D/Pd-Verhältnis reagieren und andere wiederum nicht, stellt eine wichtige Frage dar, die in einem der nachfolgenden Abschnitte beantwortet wird.

Abbildung 4. Auswirkung des D/Pd-Verhältnisses auf die Stromerzeugung bei der Reaktion einer aktiven Charge von Pd-Draht in einer Elektrolysezelle bei 20 °C. McKubre und Kollegen.

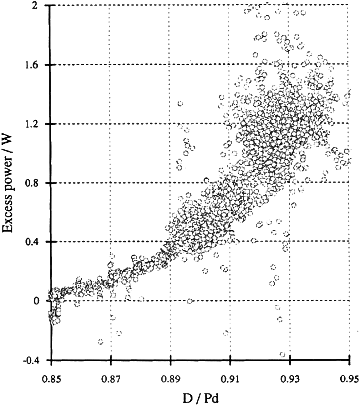
Man beachte, dass die Energieerzeugung praktisch auf null gesunken ist, sobald das D/Pd-Verhältnis bei 20 °C unter 0,85 D/Pd lag. Hätte man diese und weitere Zusammensetzungen von niedrigerem Verhältnis erhitzt, wäre vermutlich ein Energieüberschuss erzielt worden. Daher scheinen die Temperatur und das D/Pd-Verhältnis die Reaktionsrate eines Prozesses zu erhöhen, welcher bereits im Gange ist, bei dem die Leistung jedoch über die Nachweisgrenze des Kalorimeters angehoben werden müsste, um den Prozess überhaupt sichtbar zu machen.

3.4 Der Einfluss von Laserstrahlung

Die Einwirkung von Laserstrahlung auf ein Material kann vielfältige Wirkungen haben, so beispielsweise die Erhöhung der lokalen Temperatur, die erhöhte Verfügbarkeit von Elektronen sowie die Anregung von Phononen-Energiezuständen. Letts und Cravens haben herausgefunden, dass mit Au beschichtetes PdD unter der Einwirkung von 669 nm Laserstrahlung zu einer gesteigerten Erzeugung von Energie führt. Storms hat nachgewiesen, dass die Laserstrahlung den nuklearen Prozess nicht auslöst, stattdessen jedoch die Reaktionsrate eines bereits in Gang befindlichen Prozesses erhöht. In seiner Arbeit wurde auch aufgezeigt, dass zur Erzeugung von Überschussenergie eine Au-Beschichtung nicht zwingend erforderlich ist.

Später haben Letts und Kollegen zwei Laser mit variablen Frequenzen zum Einsatz gebracht. Dabei wurden mehrere Schwebungsfrequenzen ermittelt, die ihrer Meinung nach zu einer erhöhten Energieerzeugung führen. Dieses Ergebnis wurde von Hagelstein zur Untermauerung seines Phononenmodells herangezogen. Andererseits konnte diese Studie den in ihren vorangegangenen Arbeiten beobachteten Einzelfrequenzeffekt nicht bestätigen. Auch der Versuch von Guffey und anderen, diese Ergebnisse zu wiederholen, konnte den behaupteten Effekt nicht erzielen. Auch andere Forscher haben Laser mit unterschiedlichen Frequenzen eingesetzt, mit denen sich die erzeugte Energiemenge vergrößern ließ, auch ohne dass dafür eine Schwebungsfrequenz erforderlich gewesen wäre. Ein Beispiel hierfür ist der Bericht von Tian und Kollegen. Dementsprechend ist die Wirkung einer speziellen Frequenz, wie sie von Hagelstein und Letts gefordert wird, weiterhin nicht belegt.

Es wurde festgestellt, dass durch die Laserstrahlung sowohl eine Antistokes- als auch eine Maser- Strahlung hervorgerufen wird. Diese Strahlungen könnten das Ergebnis von Veränderungen innerhalb der chemischen Struktur sein, welche durch die Fusionsreaktion hervorgerufen werden, oder aber sie entspringen direkt dem nuklearen Prozess selbst. Entscheidend ist, dass dieses Verhalten darauf hindeutet, dass es im Zuge der Fusionsreaktion zu einem kohärenten Prozess kommen kann. Auf diese Überlegung wird in einem späteren Abschnitt noch näher eingegangen.

Obwohl ein Laser den nuklearen Prozess anregen kann, weiß man noch immer nicht genau, was die Gründe dafür sind.

3.5 Der Einfluss von angelegtem Strom

Es wurde festgestellt, dass die von einer elektrolytischen Zelle erzeugte Menge an Energie zunimmt, sobald der elektrolytische Strom erhöht wird. Zurückgeführt wurde dieser Effekt entweder auf die erhöhte Temperatur oder auf das erhöhte D/Pd-Verhältnis. Eine gesteigerte Energiemenge kommt auch dadurch zustande, dass der Strom im D₂-Gas durch das PdD geleitet wird. Dieses Verhalten hat man auf die Elektromigration zurückgeführt, bei der es an der negativen Elektrode zu einer Konzentration von D⁺ kommt, wodurch sich an dieser Stelle die lokale Fusionsrate erhöht.

Tanzella und Mitarbeiter sowie das Patent von Godes beschreiben die Verwendung von gepulstem elektrischen Strom mit einer sehr kurzen Anstiegszeit, um auf diese Weise in einer komplexen Festkörperstruktur einen wärmeerzeugenden Prozess anzuregen. Es wird angenommen, dass der gepulste elektrische Strom die Bildung von freien Neutronen sowie nachfolgend die Bildung von ⁴H bewirkt. Vernachlässigt wird die Notwendigkeit, dem dabei entstehenden Neutron 0,78 MeV an Energie als Massenäquivalent hinzuzufügen. Die vorgeschlagene Erklärung ist insofern nicht plausibel, als eine solche Energiemenge in einer chemischen Struktur nicht verfügbar ist.

Celani und seine Kollegen haben eine Elektrolysezelle mit gepulstem elektrischen Strom beaufschlagt, was zu einem Anstieg der Überschussenergie geführt hat. Später haben sie dann Gleichstrom eingesetzt, um Drähte aus Konstantan zu erhitzen, welche sie zu komplizierten Formen gebogen hatten. Zur Erzeugung von zusätzlicher Überschussenergie kam es, wenn sie dem noch einen gepulsten elektrischen Strom hinzugefügt haben. Dieses Verfahren wurde mit einer Erklärung begründet, die zu komplex ist, um sie an dieser Stelle zu erörtern.

Staker ließ Gleichstrom durch einen Pd-Draht fließen, währenddessen dieser in einer herkömmlichen Elektrolysezelle elektrolysiert wurde. Dabei stellte er fest, dass dieser elektrische Strom die Menge an erzeugter Energie erhöht hat. Bedauerlicherweise erklärte er sich dieses Verhalten mit einem vermeintlichen Phasenwechsel, für den es jedoch keinerlei Beweise gab.

Tanaka und Himeno sind der Ansicht, dass elektrische Ströme, sowohl spontane als auch angelegte, die Fusionsrate über eine Verstärkung des Tunnelprozesses steigern können.

All diese Erklärungen bedürfen möglicherweise einer erneuten Überprüfung, wie sie in Abschnitt 5.0 vorgenommen wird. Ungeachtet der widersprüchlichen Begründungen scheint ein angelegter Strom einen erheblichen Einfluss auf die Menge der erzeugten Energie zu haben.

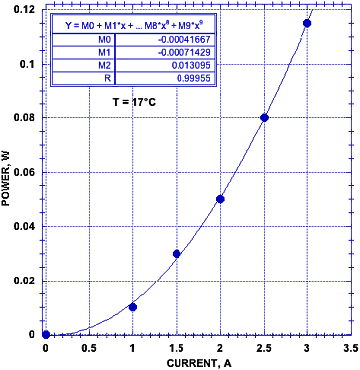
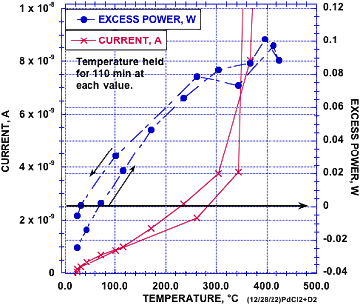
Dies hat mich veranlasst, eine Studie zu diesem Effekt zu erstellen, die hier kurz beschrieben werden soll, um damit den Anstoß zu geben für eine ausführlichere Untersuchung, welche schon möglichst bald durchgeführt werden sollte. Dazu wurde ein massives Stück Pd mit Pd plattiert, um lokale Inseln von einer komplexen Struktur zu schaffen, so wie dies von Gordon und Whitehouse (G-W) beschrieben wurde. Abbildung 5 veranschaulicht, wie das Pd zugeschnitten wurde, damit der elektrische Strom den größten Teil des Materials erreichen kann. Danach wurde die Probe in eine Zelle mit D₂-Gas bei etwa 0,5 atm platziert und wie in Abbildung 6 gezeigt erhitzt. Die geringfügige, durch den elektrischen Strom hinzugekommene Menge an Energie wurde von jener Energie abgezogen, die die Probe selbst erzeugt hat. Diese zusätzliche Energiemenge war zu gering, um eine signifikante Temperaturveränderung zu bewirken. Jedenfalls dient der Gleichstrom, welcher durch einen die Zelle umgebenden Widerstandsdraht fließt, der Temperaturerhöhung. Nähere diesbezügliche Einzelheiten werden in einem späteren Beitrag behandelt.

Abbildung 5: Pd-Probe, die mit galvanisch abgeschiedenem Pd beschichtet und so zugeschnitten ist, dass das Metall von einem elektrischen Strom durchflossen werden kann. Der Querschnitt, den der Strom durchfließt, beträgt etwa 1 mm x 3 mm. Das Pd wiegt 2,5 g. (Wird noch veröffentlicht)

Abbildung 6: Auswirkung eines konstanten Gleichstroms, welcher bei verschiedenen Temperaturen im D₂-Gas durch das PdD fließt. Die Höhe des angelegten Stroms wird in Ampere (A) angegeben. Zunächst wurden die Werte für „kein Strom“ ermittelt, anschließend die Werte, die mit „angelegter Strom“ bezeichnet werden.

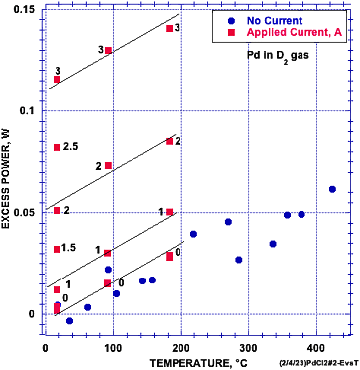
Es ist wichtig zu beachten, dass die Wirkung des angelegten elektrischen Stroms erheblich ist und mit ansteigender Stromstärke zunimmt, wie dies Abbildung 7 zu entnehmen ist. Diese Größe hat nicht nur das Potenzial, die Menge der Energie zu erhöhen, sondern könnte auch dazu genutzt werden, eine schnelle Reaktion auf eine variable Last zu ermöglichen. Darüber hinaus ist diese Größe temperaturunabhängig, und die Wirkung der angewandten Temperatur ist wiederum unabhängig von der verwendeten Stromstärke. Mit anderen Worten, die Wirkung beider Größen ist das Resultat zweier unterschiedlicher und unabhängiger Prozesse, von denen die verwendete Stromstärke die größere Wirkung besitzt. Spätere Studien haben gezeigt, dass die Pd-Abscheidung nicht notwendig dafür war, dass der elektrische Strom zu einer Erhöhung der Energiemenge führt. Der Widerstand konnte auch dazu herangezogen werden, anhand der von McKubre und Tanzella aufgestellten Gleichung das durchschnittliche D/Pd-Verhältnis zu berechnen.

Abbildung 7. Überschussenergie als Funktion der angelegten Stromstärke bei 17 °C. Zu beachten ist, dass bei fehlendem Stromfluss auch keine überschüssige Energie zu verzeichnen ist.

Eine Umkehrung des Stromflusses im Anschluss an die Untersuchung hat zu keiner Veränderung bei der Überschussenergie geführt. Dieses Verhalten deutet darauf hin, dass die durch die Elektromigration verursachte Konzentrationsänderung keine signifikante Auswirkung auf die Überschussenergie hatte. Diese vorläufige Studie muss jedoch unbedingt noch einmal wiederholt werden, um die Auswirkungen eines Magnetfeldes, eines gepulsten Gleich- oder Wechselstroms sowie der Stromdichte zu untersuchen. Der Grund dafür, dass die Stromstärke einen so großen Einfluss auf die erzeugte Energie hat, wird in einem späteren Abschnitt dargelegt.

3.6 Die Erzeugung von Helium

Man hat Helium als ein Fusionsprodukt erwartet und schließlich auch gefunden. Doch anders als jenes Helium, zu dessen Bildung es im Rahmen der Hochenergiefusion (Heiße Fusion) kommt, bleibt der Heliumkern, der bei der Kalten Fusion entsteht, intakt und lässt sich als Heliumgas nachweisen. Dies stellt jedoch insofern ein Problem dar, als es bei der hier beschriebenen Kernreaktion keine erkennbare Möglichkeit für eine Impulserhaltung gibt, wenn die erzeugte Kernenergie nach der Bildung des Heliums abgeführt wird. Für die Impulserhaltung sind zwei oder mehr nukleare Reaktionsprodukte erforderlich. Daher muss neben dem neuen Kern noch etwas weiteres freigesetzt werden, wie dies in Abschnitt 4.0 erläutert wird. Außerdem muss die Erklärung auch darüber Aufschluss geben, wieso die durch die niederenergetische Fusion freigesetzte Energie den He-Kern nicht destabilisiert, so wie es bei der Fusion von D+D mit ihrer hohen Energie der Fall ist.

Und das sind nicht die einzigen Konflikte, die bezüglich des zu erwartenden Verhaltens gelöst werden müssen. Um das He messen zu können, muss es zunächst aus dem Material herausdiffundieren und vom umgebenden D₂-Gas aufgefangen werden. Da Helium bekanntermaßen nur sehr langsam diffundiert und sich in Pd oder PdD nur sehr schlecht auflöst, erscheint es eher unwahrscheinlich, dass diese Voraussetzung erfüllt wird – es sei denn, die Heliumquelle befindet sich sehr nahe an der Oberfläche. Andernfalls würde das Helium von der PdD-Struktur eingeschlossen werden, wofür keine Messungen vorliegen. Eine reproduzierbare Freisetzung des Heliums kann nur dann erwartet werden, wenn es immer in einem ähnlichen Abstand von der Oberfläche erzeugt wird. Allerdings lässt sich die erforderliche Menge an Helium erst dann gewinnen, wenn ausreichend Zeit verstrichen ist, um die Erzeugungsrate auf die Verlustrate einzustellen, was eine beträchtliche Zeitdauer erfordern würde, um die durchschnittliche Heliumkonzentration auf einen Wert anzuheben, bei dem der Verlust der Erzeugungsrate entspricht. Es liegen keine Anhaltspunkte dafür vor, dass eine der beiden Voraussetzungen zum Zeitpunkt der in Abbildung 8 dargestellten Messungen bereits erfüllt war. Im Folgenden wird diese Verlustrate beschrieben.

Abbildung 8. Histogramm von 16 Messungen aus vier unabhängigen Studien, in denen die Heliummenge durch jene Energiemenge dividiert wurde, die durch elektrochemische Zellen unter Einsatz von D₂O erzeugt wurde. An die Werteverteilung wurde eine Gaußsche Fehlerfunktion angepasst. Dargestellt ist das Verhältnis auf der Grundlage der Massenänderung für die Fusionsreaktion D + D = ⁴He. Der von McKubre und Kollegen ermittelte Wert stammt von einer Probe aus Holzkohle, auf die eine kleine Menge an Pd aufgebracht wurde. Diese Probe wurde unter D₂-Gas auf 243 °C erhitzt.

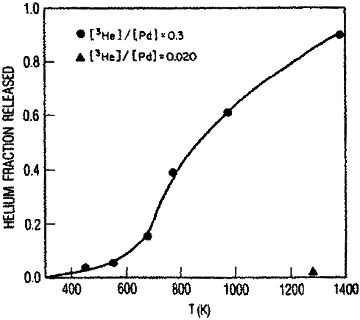
Die Verlustrate des He aus dem Pd wurde von Abell und Kollegen untersucht, die den Verlust von ³He aus dem Pd anhand des Zerfalls von Tritium gemessen haben. Sie hatten herausgefunden, dass die Fähigkeit von He, das Pd zu verlassen, im Zusammenhang mit der He-Konzentration steht, wobei eine Temperatur von mindestens 1300 K erforderlich ist, um das He vollständig zu entfernen, und dies bei einem He/Pd-Verhältnis von 0,02, so wie in Abbildung 9 dargestellt. Die durchschnittliche He-Konzentration während einer typischen Messung (Abbildung 8) läge bei etwa 10^-11 He/Pd und die Temperatur bei etwa 300 K. Selbst wenn die Erzeugung des Heliums sehr nahe an der Oberfläche erfolgt, würde mindestens die Hälfte im Material verbleiben, denn ein Teil des nuklearen Reaktionsprodukts würde von der Oberfläche wegdiffundieren. Diese Überlegungen haben zur Folge, dass das beobachtete Verhalten des ⁴He nur schwer zu erklären ist. Eine Lösung für diesen Konflikt wird in Abschnitt 4.3.2 vorgestellt.

Abbildung 9. Anteil des freigesetzten Heliums als Funktion der Temperatur für zwei unterschiedliche He/Pd-Verhältnisse. Aus Abell und Kollegen.

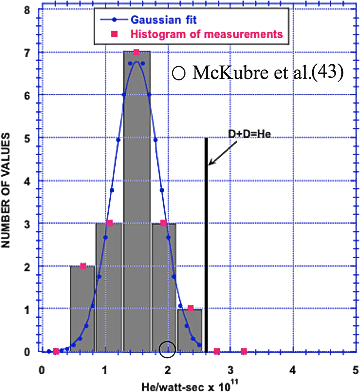
Die Quelle des He lässt sich dadurch ermitteln, dass man das gemessene He/Energie-Verhältnis mit jenem Wert vergleicht, der sich im Zuge der Umwandlung von D+D in He aus der Massenänderung errechnet, die einen Wert von 2,6 × 10¹¹ He/Wattsekunde ergibt. Dieser Wert ist in Abbildung 8 als vertikale Linie aufgetragen und stellt die Rate dar, mit der das He gebildet wird, wobei die gemessene Energiemenge mit der gemessenen Heliummenge verglichen und als He/Wattsekunden-Verhältnis in Abbildung 8 eingetragen wird. In diesem Histogramm werden sechzehn separate Messungen aus vier unabhängigen Studien zum Helium in jenem Gas verglichen, welches in einer elektrolytischen Zelle mittels einer PdD-Kathode erzeugt wurde. Da das in der Kathode eingeschlossene Helium nicht mitgemessen wurde, ist davon auszugehen, dass das Verhältnis kleiner als der tatsächliche Wert ist, was im vorliegenden Fall auch zutrifft.

Darüber hinaus steht das Gesamtverhalten im Einklang mit einer Fehlerfunktion, wie sie sich in jeder Messung aus kleinen zufälligen Fehlern ergeben würde – wobei sieben der sechzehn Messungen zeigen, dass etwa die Hälfte des erzeugten He im PdD gebunden bleibt. Da die Mengen an Energie und an Helium aus unabhängigen Messungen stammen, deutet diese Form der Übereinstimmung darauf hin, dass sowohl die Energie als auch das Helium aus einer gemeinsamen Quelle stammen und nicht aus einer zufälligen Kombination von zufälligen Fehlern in jeder Messung von Energie und Helium. Eine derartige konsistente Kombination von zufälligen Fehlern in den unabhängigen Messungen von Energie und Helium wäre sehr unwahrscheinlich, insbesondere wenn die Messungen, basierend auf der Massenänderung, mit dem erforderlichen Verhältnis übereinstimmen.

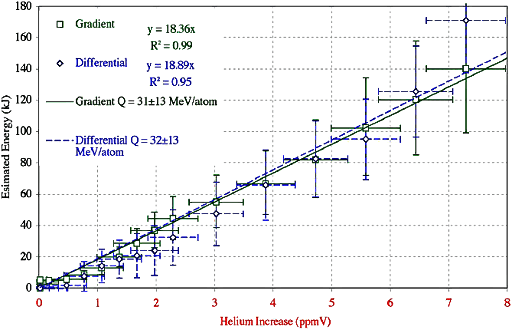
Im Unterschied zu den in Abbildung 8 verglichenen Messungen haben McKubre und Kollegen das Helium gemessen, das aus einer Probe einer speziellen Kokosnusskohle gewonnen wurde, in der kleine Pd-Partikel enthalten waren, welche im D₂-Gas erhitzt wurden, das durch die Case zur Verfügung gestellt wurde. Die Messung der erzeugten Energiemenge erfolgte mit zwei unterschiedlichen Kalorimetertypen: einem Gradienten- sowie einem Differentialkalorimeter. Die Messung der Heliummenge erfolgte mittels eines Massenspektrometers in Echtzeit. Der konstante Anstieg der Leistung und des He-Gehaltes belegt, dass sich hier ein stationärer Zustand eingestellt hat. Ein Luftleck als Quelle des Heliums ist ausgeschlossen, denn die Menge des Heliums übersteigt schließlich dessen Konzentration in der Luft. Abbildung 10 veranschaulicht die sich ergebende Beziehung zwischen Energie und Helium, wobei sowohl die Helium- als auch die Energiemenge mit der Zeit zunehmen. Eine deutliche Übereinstimmung mit anderen Messungen zeigt sich, wenn man das durchschnittliche He/Wattsekunden-Verhältnis (siehe den Gradienten in Abbildung 10) von 2,0 ± 0,8 x 10¹¹ mit jenen Werten vergleicht, welche durch die Elektrolyse gewonnen wurden (siehe Abbildung 8). Der Umstand, dass andere Holzkohlequellen eine Fusionsreaktion nicht unterstützt haben, deutet jedoch darauf hin, dass sich die Fusionsreaktion eher in der Holzkohle selbst ereignet hat als im Pd. Das gesamte in dieser Probe verbliebene Helium konnte nach wiederholter Reaktion mit D₂ in einem Vakuum ausgewaschen werden, was bedeutet, dass die mit jeder He-Bildung erzeugte Menge an Energie dem aus der D+D-Fusion resultierenden Massenverlust entsprach. Die große Anzahl von Werten, die eine konsistente Beziehung aufweisen, lässt darauf schließen, dass diese Werte das gesamte He und die gesamte Energie, welche im Zuge einer Fusionsreaktion mit Deuterium entstehen, widerspiegeln.

Abbildung 10. Die Energie und das Helium wurden aus einer speziellen Charge von Kokosnusskohle gewonnen, auf die man 5 % Pd in Form von feinsten Partikeln aufgetragen und bei 243 °C unter D₂-Gas erhitzt hat, während die Energie und das Helium gemessen wurden – wie McKubre und Kollegen berichten.

3.7 Die Erzeugung von Tritium

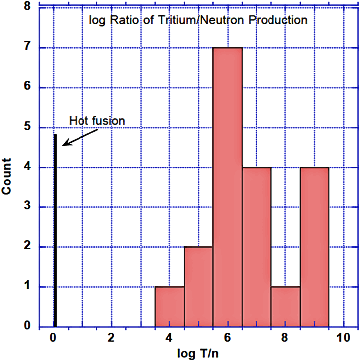
Bei Tritium handelt es sich um ein unbedeutendes nukleares Reaktionsprodukt, das im Rahmen der Kalten Fusion nur äußerst selten und nur unter ganz bestimmten Bedingungen zustande kommt. Dennoch weist bereits sein gelegentliches Auftreten auf die Existenz eines ungewöhnlichen nuklearen Prozesses hin, der sich normalerweise gar nicht ereignen sollte. Im Gegensatz zu dem Tritium, das bei der Hochenergiefusion (Heiße Fusion) entsteht, wird dieses Tritium nicht von einer gleich großen Anzahl an Neutronen begleitet. Stattdessen dominiert das Tritium die Neutronen in einem Verhältnis, wie es in Abbildung 11 wiedergegeben wird. Ob die große Bandbreite der Werte auf einen Fehler zurückzuführen ist oder ob eine weitere unbekannte Größe im Spiel ist, lässt sich nur schwer feststellen. Jedenfalls würde die Klärung dieser Frage einen weiteren Einblick in diese ungewöhnliche nukleare Reaktion gewähren, wie in einem späteren Abschnitt noch erörtert wird, und damit die angestrebte Erklärung weiter stützen.

Abbildung 11. Histogramm der veröffentlichten Messungen des logarithmischen Tritium/Neutronen-Verhältnisses. Der gemessene logarithmische T/n-Wert aus der Heißen Fusion ist ebenfalls eingezeichnet. Die Werte entstammen der Tabelle 6 in „The Science of Low Energy Nuclear Reaction“.

3.8 Die Strahlung

Bei den meisten nuklearen Ereignissen wird die Energie über Strahlung abgegeben. Obwohl man immer wieder danach gesucht hat, konnte man bei der Kalten Fusion außerhalb der entsprechenden Versuchsanlagen nur sehr selten irgendwelche Strahlung feststellen. Diese offensichtliche Abwesenheit hat zu großer Verwirrung und zu zahlreichen Spekulationen über die Frage geführt, auf welche Weise die Kernenergie abgeführt wird und wodurch die Impulserhaltung gewährleistet ist. Eine eingehendere Untersuchung hat allerdings gezeigt, dass tatsächlich eine Strahlung emittiert wird, deren Energie jedoch zu gering ist, um aus der Anlage austreten zu können. Darüber hinaus weist diese Strahlung einige recht ungewöhnliche Eigenschaften auf, die im Folgenden beschrieben werden.

Da es zu keiner gefährlichen Strahlung kommt, lässt sich die erzeugte Energie gefahrlos untersuchen und nutzen.

3.8.1 Die Ionenemission

Man ging selbstverständlich davon aus, dass das beobachtete Heliumgas (Abbildung 8) zusammen mit dem Großteil der nuklearen Energie emittiert wird, vergleichbar mit der klassischen Emission von Alphateilchen. Karabut und Kollegen (K-K) haben das Ionenspektrum gemessen, wie es bei einer Gasentladung unter D₂ entsteht. Zur Bestimmung der Energie der Ionen sowie zum Nachweis der Anwesenheit energiereicher Ionen kam ein Siliziumbarrieredetektor (SBD) zum Einsatz, der auf der Basis von CR-39 gearbeitet hat. Das Energiespektrum bestand aus zahlreichen separaten Peaks mit nahezu gleichem Abstand, deren Intensität mit zunehmender Energie abgenommen hat. Der größte Teil der aufgezeichneten Energie lag im Bereich zwischen 1 MeV und 6 MeV. Diese Strahlung dauerte auch nach dem Abschalten der Gasentladung weiter an, was auf einen fortgesetzten Fusionsprozess hindeutet. Die augenscheinliche Emission war also nicht das Ergebnis des von der Entladung erzeugten elektrischen „Rauschens“. Die Forscher gingen davon aus, dass diese Strahlung auf Alphastrahlung zurückzuführen ist, da im Anschluss an das Experiment in der Pd-Kathode noch ⁴He nachgewiesen worden war. Neben einem geringen Neutronenfluss im Zuge der Entladung wurde im Gas auch eine geringe Menge an Tritium nachgewiesen. Darüber hinaus wurden Photonen mit laserähnlichen Eigenschaften emittiert. Dieses Verhalten ist für einen „normalen“ Kernprozess eher untypisch.

Abbildung 12 stellt für alle von K-K erfassten Werte die Beziehung zwischen der Höchstzahl und der Ionenenergie dar. Man erkennt zwei unterschiedliche Verhaltensweisen, die für sich genommen zwischen der Ionenenergie und der Abfolge jeweils eine lineare Beziehung aufweisen.

Abbildung 12. Ionenenergie gegenüber der Anzahl der Ionen in der von K-K angegebenen Abfolge.

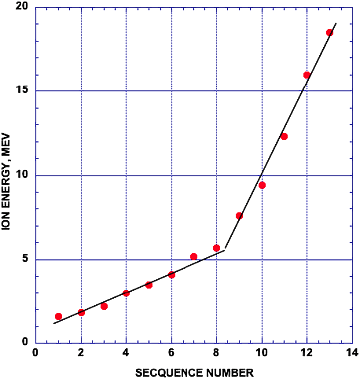
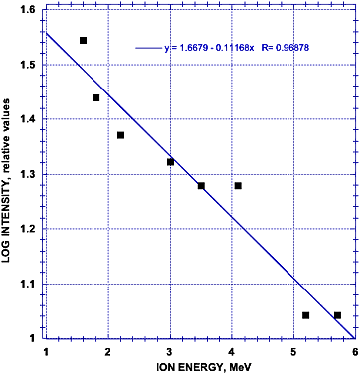
Wie Abbildung 13 zeigt, nimmt der Ionenfluss mit zunehmender Energie ab, sodass sich beim Auftragen des logarithmischen Peakwertes als Funktion der Maximalenergie für die Ionenenergie bis zu 6 MeV eine lineare Beziehung ergibt. Ionen mit höheren Energien weisen sogar noch geringere Emissionen auf. Die Auswirkungen dieses Verhaltens werden in Abschnitt 3.8 diskutiert.

Abbildung 13. Logarithmus der relativen Intensität der Ionenemission gegenüber der von K-K genannten Energie für Energien kleiner als 6 MeV.

Acht Jahre später haben Storms und Scanlan (S-S) das Ionenspektrum gemessen, allerdings über einen kleineren Energiebereich (Abbildung 14), erneut erzeugt mittels Gasentladung und unter Einsatz eines Siliziumbarrieredetektors. Bei dieser Messung wurden zwischen der Quelle und dem Detektor Absorber angebracht, um so auf die wahre Natur der Ionen schließen zu können und um zu belegen, dass diese nicht das Ergebnis eines durch die elektrische Entladung erzeugten „Rauschens“ sind. Die durch elektronisches Rauschen verursachten Signale würden durch das Einfügen von derart dünnen Absorbern nicht beeinflusst werden. Stattdessen führte der Absorber bei jedem Peak zu einer reproduzierbaren Reduzierung der gemessenen Energie, die dann zur Identifizierung des emittierten Elements herangezogen werden konnte.

Abbildung 14. Kommt entweder H₂ oder D₂ zum Einsatz, ergibt sich bei der Gasentladung ein typisches Spektrum. Die BIN-Nummer wurde anhand des Alphaspektrums kalibriert, welches von Po-210 emittiert wird. Die Zählungen bei BIN-Nummern unter 200 werden durch das „Rauschen“ verursacht, welches von der elektrischen Entladung erzeugt wird. (MeV=0,000657 * BIN)

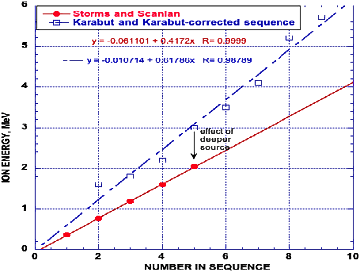
Das Vertrauen in diese wie auch in die von K-K gemeldete Messung rechtfertigt sich durch die gute Übereinstimmung zwischen der berichteten Strahlungsenergie einerseits und den einzigartigen Charakteristika des Spektrums andererseits, welche bei diesen beiden unabhängigen Messungen festgestellt wurden. Die von K-K gemeldeten Energiewerte kommen in Abbildung 15 für einen ähnlichen Energiebereich zum Tragen, wobei dem ersten Peak der Sequenz ein Wert von 2 zugewiesen wurde, wodurch die Gleichung der kleinsten Quadrate für die Sequenz Nummer 0 eine Extrapolation der Energie nahe null liefert. Der Unterschied könnte darauf zurückzuführen sein, dass die von S-S detektierten Ionen auf einem tieferen Niveau erzeugt werden, was zu einem Energieverlust führen würde, wenn sie durch mehr Material hindurchgehen, wie der Richtungspfeil in der Abbildung verdeutlicht.

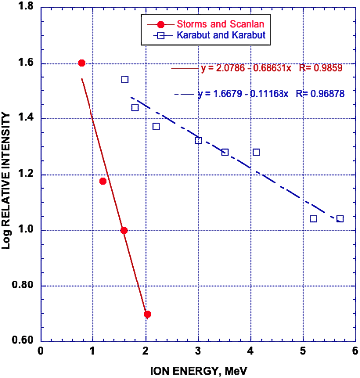
Wie Abbildung 16 zu entnehmen ist, weisen beide Studien auch bezüglich der Intensität und der Energie der einzelnen Peaks eine logarithmische Beziehung auf, wenngleich ihre Steigungen doch recht deutlich voneinander abweichen. Dieser Unterschied könnte darauf zurückzuführen sein, dass die Atomkerne und die Elektronen einen unterschiedlich leichten Zugang zur Fusionsstelle haben.

Im Falle der S-S-Studie

1. blieb das Spektrum unverändert, egal ob H₂ oder D₂ zur Anwendung kam;
2. zeigt die durch die eingefügten Absorber verursachte Energieänderung, dass es sich bei den Ionen um ein Wasserstoff- und nicht um ein Heliumisotop handelt und dass die Peaks somit nicht das Resultat von elektrischem „Rauschen“ sind;
3. ist die Ionenenergie ist zu groß, um durch einen chemischen Prozess hervorgebracht worden zu sein;
4. ist in dieser Strahlung nur ein Bruchteil jener Energie enthalten, die bei einer Fusionsreaktion freigesetzt wird.

Abbildung 15. Die Beziehung zwischen der Sequenz im Spektrum und der Ionenenergie. Die Werte wurden aus den Abbildungen 12 und 14 entnommen. Der Richtungspfeil stellt die Auswirkung auf die Energie dar, die beim Durchgang durch ein absorbierendes Material entsteht. Die Sequenznummer wurde für die K-K-Werte so korrigiert, dass die Energie bei der Sequenznummer 0 gleich 0 ist, da der erste Peak in dieser Reihe im Rauschen untergeht.

Ionen, die tiefer als einige Mikrometer unter der Oberfläche entstehen, würden nicht nachgewiesen werden können. Wenn die Ionen aus vielen verschiedenen Quellen stammen würden, die sich alle in unterschiedlichen Tiefen befinden, wäre das Spektrum verschmiert und jeder Peak würde einen breiten Wertebereich aufweisen. Die ähnliche Breite der einzelnen Peaks würde auf eine geringe, aber vergleichbare Streuung zurückzuführen sein. Natürlich könnten Ionen auch an anderen Stellen erzeugt werden, doch wären diese zu tief gelegen, als dass die Ionen den Detektor erreichen könnten. Zudem würden nur solche Ionen erfasst, die in eine bestimmte Richtung emittiert werden. Diese Überlegungen deuten darauf hin, dass die in beiden Studien detektierten Ionen aus einer einzigen, sehr oberflächennahen Quelle stammen.

Abbildung 16. Die Beziehung zwischen logarithmischer Intensität und Ionenenergie. Da die Intensität einen relativen Wert zur Grundlage hat, ist lediglich die Differenz der Steigung von Bedeutung. Die Werte für S-S wurden der Abbildung 14 entnommen.

Aus welchem Grund jeder Peak die gleiche Energiedifferenz gegenüber seinem Nachbarn aufweist, stellt nach wie vor ein Rätsel dar. K-K fanden heraus, dass diese konstante Differenz größer ist (0,617 MeV) als der von S-S angegebene Wert (0,417 MeV). Möglicherweise erfuhren die von K-K gemessenen Ionen einen geringeren Energieverlust, da sie näher an der Oberfläche erzeugt wurden als die von S-S gemessenen Ionen.

Das Verhalten deutet darauf hin, dass durch einen noch unbekannten Prozess ein quantisiertes Verhalten hervorgerufen wird, bei dem die einzelnen Peaks nacheinander beeinflusst werden und nicht durch ein einzelnes Ereigniss, das sämtliche Emissionen einschließt. Das Rätsel wird noch dadurch vergrößert, dass sich die Ionenenergie nicht in einem eindeutigen Verhältnis zu jener Gesamtenergiemenge befindet, welche durch die Fusionsreaktion freigesetzt wird. Eine Erklärung hierfür wird im nächsten Abschnitt vorgestellt.

Das sehr ähnliche Verhalten von H₂ und D₂ stellte, als es von S-S entdeckt wurde, eine große Überraschung dar. Dies lässt den Schluss zu, dass beide Reaktanten das gleiche nukleare Reaktionsprodukt erzeugen können. Allerdings kann aus diesem Verhalten nicht geschlossen werden, dass nicht gleichzeitig auch andere nukleare Reaktionsprodukte erzeugt werden, deren Emissionen jedoch unentdeckt bleiben, da ihre Energie nicht in den Bereich des SBD (Siliziumbarrieredetektor) fallen würde. Eine Erklärung dafür wird in einem späteren Abschnitt erörtert.

S-S bestimmten die Beschaffenheit der Ionen durch die Messung der Energieänderung, welche beim Einsatz verschiedener Absorber auftritt. Die gemessene Energieänderung wurde dann mit den in den NIST-Tabellen (NSRDS-NBS29) beschriebenen Werten verglichen, um auf diese Weise das emittierte Element zu identifizieren. Dabei hat sich gezeigt, dass die Emissionen mit den Ionen eines Wasserstoffisotops übereinstimmen, nicht aber mit denen des Heliums! Zum Zeitpunkt der Studie wurde die Emission von ⁴H, die mit dem beobachteten Verhalten übereinstimmt, jedoch nicht in Betracht gezogen.

Bei der Fusion von D wird eine Energie in Höhe von 23,84 MeV freigesetzt, die unter Erhaltung des Impulses dissipiert werden muss. Das emittierte nukleare Reaktionsprodukt weist nur einen Bruchteil dieser Energie auf. Wo ist die fehlende Energie? Außerdem erfordert die Impulserhaltung die gleichzeitige Emission von zwei Teilchen. Wo ist das andere Teilchen? Wieso verteilt sich die Energie auf viele diskrete Energien? Diese Fragen ergänzen die wachsende Liste jener Fragen, für die eine Erklärung gefunden werden muss, so wie in Abschnitt 4.0 beschrieben.

In über einhundert Studien wurde die Ionenemission in elektrolytischen Zellen unter Verwendung von CR-39 gemessen, um sowohl ihre Existenz nachzuweisen als auch ihre Energie zu bestimmen. In allen Untersuchungen wurde davon ausgegangen, dass die im CR-39-Kunststoff hervorgerufenen Flecken auf die Emission von ⁴H zurückzuführen sind, wobei die entsprechende Energie auf der Basis der Alphastrahlung von Quellen mit bekannter Energie kalibriert wurde. In Anbetracht der von K-K und S-S durchgeführten Untersuchungen könnten diese Flecken jedoch auch auf ⁴H-Emissionen zurückzuführen sein. Ein ⁴H-Ion hätte Flecken von anderer Größe erzeugt als ein Alpha-Ion von gleicher Energie. Folglich könnte die angegebene Energie, die auf dieser Kalibrierung beruht, falsch sein. Diese Möglichkeit muss ernsthaft in Erwägung gezogen werden.

Die emittierten ⁴H-Ionen verfügen über genügend Energie, um Kernreaktionen in Form von Transmutation und Heißer Fusion auszulösen, die zu unerwarteter Strahlung führen könnten. Diese Möglichkeit wird im weiteren Verlauf dieses Artikels noch erörtert.

3.8.2 Die Photonenemission

Um die von einer Kathode ausgehenden, stark gebündelten Photonenstrahlen aufzuzeichnen, haben Karabut und Kollegen einen fotografischen Film verwendet. Darüber hinaus haben sie die Energie der Photonen gemessen und dabei festgestellt, dass sich diese Strahlung wie ein Laser verhält. Die Energie der Photonen entspricht sowohl der einer nuklearen Quelle als auch der Energie von Röntgenstrahlen. Ein Teil der Strahlung resultierte sogar aus einem radioaktiven Zerfall, der sich über viele Stunden hinweg vollzog. Wurden zwischen die Kathode und die fotografische Platte wahlweise 0,5 mm Aluminium oder 2 mm Blei platziert, zeigte sich bei der Photonenemission ein ähnliches Muster dessen, was in Abbildung 17 dargestellt ist. Offensichtlich werden Photonen mit einem breiten Energiespektrum als stark gebündelte Strahlen mit unterschiedlicher Intensität in zufällige Richtungen emittiert. Die Auswirkungen dieses Verhaltens sind komplex und bedeutsam, wie in Abschnitt 4.3 erläutert wird.

Abbildung 17. Nach dem Durchgang von Photonen durch 0,5 mm Aluminium erscheinen auf einem Fotofilm Flecken. Ein ähnliches Muster entsteht, wenn 2 mm Pb verwendet wird, was darauf hinweist, dass die Strahlung ein breites Energiespektrum umfasst.

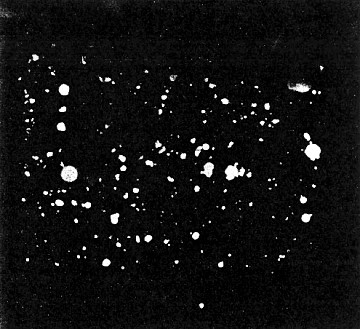
Szpak und andere hatten ebenfalls einen Fotofilm verwendet, um die Photonenstrahlung zu detektieren, wie sie von einer einzelnen, genau definierten Quelle ausging, im konkreten Fall jedoch von einer elektrolytischen Zelle. Auch hierbei wurde eine Photonenstrahlung mit einem ähnlich ungewöhnlichen Verhalten beobachtet.

Weil man im Zusammenhang mit einem nuklearen Prozess keine stark gebündelten Photonenstrahlen erwarten würde, kamen bei den meisten bisherigen Studien, in denen eine Photonen- oder Elektronenstrahlung nachgewiesen wurde, keine Verfahren zum Einsatz, mit denen sich gebündelte Strahlung nachweisen lässt, so dass dieses ungewöhnliche Verhalten überhaupt nicht bemerkt worden ist. Dieses Versäumnis ist insofern von Bedeutung, als dass dieses einzigartige Verhalten das Potenzial besitzt, uns Aufschluss über jenen Mechanismus zu geben, durch den die Kernenergie freigesetzt wird, wie nachfolgend beschrieben.

3.8.3 Die Elektronenemission

Zur Emission von Elektronen kommt es in der Regel dadurch, dass sich im Atomkern die Umwandlung eines Neutrons in ein Proton vollzieht. Dieser Vorgang wird auch als Betazerfall bezeichnet. Tritium ist so ein Betastrahler.

Kürzlich haben Gordon und Whitehouse (G-W) einen starken Elektronenstrom gemessen, der durch eine Pd-Ablagerung emittiert wurde, welche D₂ ausgesetzt war, sowie durch eine Fe-Ablagerung, die H₂ ausgesetzt war. Diese Emission ist nicht auf eine Betastrahlung zurückzuführen, die auf irgendeiner Halbwertzeit basiert. Vielmehr kommt es zu diesem kontinuierlichen Strom von energiereichen Elektronen dadurch, dass dieser durch ein Material emittiert wird, das bekanntermaßen die Kalte Fusion begünstigt. Diese Messung könnte somit das letzte fehlende Puzzleteil liefern, das uns die Tür zu einem neuen Verständnis darüber aufstößt, wie es zur Dissipation nuklearer Energie kommt und wie bei der Kalten Fusion die Impulserhaltung gestaltet ist.

Um zu ergründen, ob es einen Zusammenhang zwischen dieser Elektronenemission und jener Überschussenergie gibt, die durch die Kalte Fusion erzeugt wird, habe ich die Beziehung zwischen der Elektronenemission und der Wärmeerzeugung mit Hilfe eines aktiven Materials sowie mit einem Kalorimeter untersucht, wie dies bereits in einem früheren Aufsatz beschrieben wurde: Ein Stück Pd wurde durch Aufbringen einer Pd-Schicht mittels des Co-Position-Verfahrens (CoD) nach der von G-W angewandten Methode aktiviert. Dieses Material wurde dann im D₂-Gas zusammen mit einer weiteren Elektrode aus Pt platziert, die dem Einfangen der Elektronenemission diente. Diese Anordnung aus Kollektor und Emitter wird in Abbildung 18 dargestellt. Die gesamte Anordnung ist in einer Quarzzelle eingeschlossen, die durch einen außen herum angebrachten Widerstandsdraht beheizt werden kann. Die Stromstärke wird über die Spannung gemessen, welche an einem Widerstand mit einem Wert von 0,1 MΩ anliegt.

Abbildung 18. Foto der Anordnung aus Probe und Kollektor.

Das Material wurde in einem D₂-Gas über einen Temperaturbereich hinweg erhitzt, so wie in Abbildung 19 dargestellt. Sowohl die Überschussenergie als auch der Strom der Elektronen nehmen mit ansteigender Temperatur zu, was auf eine gemeinsame Ursache hindeutet.

Abbildung 19. Messung der Überschussenergie und des emittierten Elektronenstroms in Abhängigkeit von der Temperatur im Zuge der Erwärmung von co-abgeschiedenem Pd im D₂-Gas. Zwischen den beiden Elektroden war kein externes Potenzial angelegt. Die Pfeile zeigen die Reihenfolge der Messungen an. Die Überschussenergie wurde gemessen, noch bevor die Stromstärke gemessen wurde. Die Messung der Stromstärke erfolgte erst, nachdem die Temperatur erhöht und anschließend wieder gesenkt worden war. Gemessen wurde die Temperatur nahe der Probe im Inneren der Zelle.

Diese Messungen gestalten sich weitaus komplexer, als es eine einfache Analyse vermuten lassen würde. Beispielsweise können aus der Probe Elektronen nur dann entweichen, wenn die Fusionsreaktion sehr nahe der Oberfläche erfolgt, während die Messung der Wärmeenergie ganz unabhängig davon erfolgen kann, an welcher Stelle sie erzeugt wird. Da es sich um zwei unterschiedliche chemische Umgebungen handelt, könnten diese beiden Stellen durch die Temperatur auf sehr unterschiedliche Weise beeinflusst werden. Darüber hinaus kann es zur Erzeugung von elektrischem Strom kommen, wenn die emittierten Elektronen im D₂-Gas zur Bildung von Ionen führen. Auch eine Erhöhung der Temperatur könnte zu einem gewissen Stromanstieg infolge thermionischer Emissionen führen. Für unsere Diskussion gehen wir davon aus, dass die Stromstärke, die bei Temperaturen von unter 350 °C gemessen wurde, nur auf jene Elektronen zurückzuführen ist, die durch einen nuklearen Prozess emittiert wurden und die in der Lage waren, die Oberfläche unter einem unbekannten Maß an Verminderung ihrer ursprünglichen Energie zu verlassen.

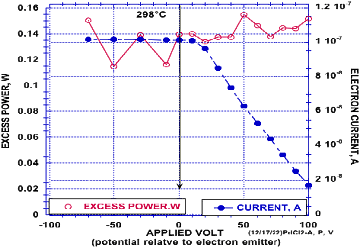
Es wurde auch der Versuch unternommen, die Energieverteilung des emittierten Stroms zu ermitteln. Dazu wurden in einer Zelle mit D₂ zwischen der Probe und dem Kollektor zunächst 100 V angelegt, während die Zelle auf 298 °C gehalten wurde. Dann wurde die Probe im Verhältnis zum Kollektor auf das in Abbildung 20 gezeigte negative Potenzial gebracht, indem beide über einen Widerstand an eine Spannungsversorgung angeschlossen wurden. Dieses Potenzial sollte sicherstellen, dass alle emittierten Elektronen unabhängig von ihrer Energie die Oberfläche verlassen und als Strom abgeleitet werden können, welcher am Widerstand in Form einer Spannung messbar sein sollte. Die im Gas befindlichen Ionen würden zu diesem Strom beitragen, dessen Größe sich ändert, sobald das Potenzial weniger negativ ausfällt. Die Tatsache, dass sich der Strom bei einem Absinken der Spannung auf null nicht ändert, weist darauf hin, dass die Gasionisierung selbst keine signifikante Stromquelle darstellt.

Wird die Spannung der Probe im Verhältnis zum Kollektor positiv eingestellt, kehren die Elektronen in die Probe zurück, solange das angelegte Potenzial gleich oder größer als deren Energie ist. Die Verringerung des emittierten Stroms (Abbildung 20) bei positiver werdender Spannung im Vergleich zur Probe zeigt, dass die emittierten Elektronen über ein bestimmtes Energiespektrum verfügen, das zum größten Teil unterhalb von 100 V liegt. Allerdings entspricht diese Energie nicht unbedingt der tatsächlichen Energie jener Elektronen, die durch den Kernprozess selbst emittiert werden, da die eingefangenen Elektronen möglicherweise durch ausreichend Material gegangen sind, um eine unbekannte Menge ihrer Energie verloren zu haben. Spätere Messungen haben gezeigt, dass die Energie der emittierten Elektronen mitunter 100 V übersteigen kann. Diese Energiemenge kann unmöglich aus einer konventionellen Quelle wie etwa einer chemischen Reaktion stammen, weil die dort freigesetzten Elektronen über eine Energie von nur wenigen eV verfügen.

Abbildung 20. Der Elektronenfluss und die Überschussenergie bei einer Temperatur von 298 °C, gemessen zwischen Emitter und Kollektor bei veränderter Spannung. Das Potenzial wird in Relation zur Probe angezeigt, wodurch jene Elektronen, die eine zusätzliche Energie aufweisen, aus der Probe emittiert werden, sobald die gemessene Spannung einen negativen Wert annimmt.

Darüber hinaus stellt die von Gordon und Whitehouse angegebene Leistung nur diejenige dar, die dissipiert wird, wenn der Strom durch eine Last geleitet wird. Diese Leistung repräsentiert nicht die gesamte von den emittierten Elektronen transportierte Energie, da der Großteil ihrer kinetischen Energie in Form von Wärme freigesetzt werden würde, sobald sie im Elektronenkollektor aufgehalten werden. Es stellt sich also wieder einmal die Frage: „Wie kommt es dazu, dass so viele energiereiche Elektronen erzeugt werden?“

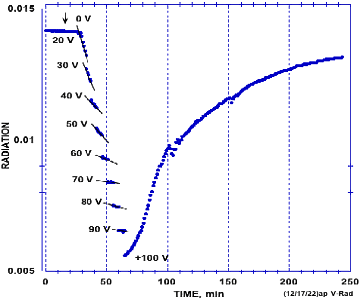
Abbildung 21 zeigt, wie sich der Strom über die Zeit verändert, wenn die angelegte Spannung erhöht wird. Nach jeder Spannungssteigerung nimmt der Strom mit einer Geschwindigkeit ab, die von der Höhe der angelegten Spannung abhängt – mit Ausnahme bei 100 V. Sobald 100 V angelegt werden und dadurch ein erheblicher Teil des Stroms zur emittierenden Oberfläche zurückfließt, steigt die Menge des emittierten Stroms rasch an, begleitet von einem geringen Anstieg der Überschussenergie. Dieses Verhalten offenbart einen weiteren unerwarteten Hinweis, auf den in einem späteren Abschnitt eingegangen wird.

Abbildung 21. Der Einfluss der Zeit auf die an einem Reihenwiderstand gemessene Spannung, während die Spannung über der Zelle, wie in Abbildung 20 dargestellt, verändert wird. Die mit „Strahlung“ gekennzeichnete Ordinate bildet für den Elektronenstrom einen relativen Wert.

Basierend auf der gemessenen Energie beträgt die Gesamtzahl aller Fusionsereignisse 3,9 × 10¹⁰ Fusionen pro Sekunde. Der gemessene Strom lässt darauf schließen, dass es den Elektronen gelingt, mit einer Rate von 6,2 x 10¹¹ Elektronen/Sekunde zu entweichen, was eine Untergrenze für die Gesamtzahl aller aus den nuklearen Ereignissen freigesetzten Elektronen darstellt. Wenn wir davon ausgehen, dass die Hälfte aller emittierten Elektronen gar nicht erfasst werden kann, weil sie ins Innere emittiert werden, ergibt sich ein Verhältnis der (Anzahl der Elektronen) zur (Anzahl der Fusionsereignisse) von 32. Dieses Verhältnis ist von Bedeutung, weil es deutlich macht, dass mehr Elektronen emittiert werden als sich Fusionen ereignen – aber weitaus weniger, als in Abschnitt 4.3.3 berechnet wird. Die Differenz ergibt sich daraus, dass die meisten der emittierten Elektronen noch vor dem Verlassen des Materials aufgehalten werden.

Und wenn diese Elektronen durch den Fusionsprozess entstanden sind, wieso werden dann im Vergleich zur Anzahl der Fusionsereignisse so viele mehr emittiert? Eine Antwort darauf folgt weiter unten.

4.0 Ein vorgeschlagenes Verfahren

Nachdem in den vorangegangenen Abschnitten die einzelnen Puzzleteile bestimmt wurden, ist es nun an der Zeit, sie zusammenzufügen. Zunächst müssen jedoch einige grundlegende Annahmen getroffen werden. Eine dieser Annahmen besteht in einer Überzeugung, die zwar nicht bewiesen werden kann, für das Vorankommen einer Theorie aber als gegeben akzeptiert werden muss. Die Plausibilität der Annahmen kann erst nachgewiesen werden, wenn sich die vorgeschlagene Theorie als richtig erweist. Sollte eine der Annahmen falsch sein, wären auch alle darauf basierenden Schlussfolgerungen fehlerhaft. Der Erfolg hängt davon ab, dass eine Annahme nur dann zur Anwendung kommt, wenn sie notwendig ist, und dass die Gründe für die Verwendung einer Annahme klar dargelegt werden müssen. Mit anderen Worten: Die gewählten Annahmen entscheiden darüber, ob eine Erklärung erfolgreich sein wird – vergleichbar der Annahme, dass der Kompass die korrekte Richtung nach Norden angibt, was wiederum ausschlaggebend dafür ist, dass bei der Erkundung einer unbekannten Gegend der richtige Weg eingeschlagen wird.

4.1 Die Annahmen

Im Folgenden werden die hier zugrunde gelegten Annahmen dargelegt.

1. Für die Kalte Fusion gelten die Gesetze der Thermodynamik, die Phasentheorie, die Regeln der Kristallbildung sowie alle chemischen Erkenntnisse. Begründung: Die Kalte Fusion ereignet sich in einer chemischen Umgebung, für die diese Regeln gelten.
2. Für die Kalte Fusion gelten der Impulserhaltungssatz, die Regeln der Quantenmechanik sowie das konventionelle Verständnis der Kernphysik. Begründung: Die Kalte Fusion stellt eine Variante des konventionellen nuklearen Verhaltens dar.
3. Für alle Wasserstoffisotope gelten derselbe universelle Mechanismus und dieselben notwendigen Bedingungen. Die verschiedenen Wasserstoffisotope erzeugen unterschiedliche Kernreaktionsprodukte über denselben Mechanismus. Begründung: Alle Wasserstoffisotope weisen sehr ähnliche chemische Eigenschaften auf, die den Fusionsmechanismus steuern.
4. Unabhängig davon, welches Wirtsmaterial zum Einsatz kommt und auf welche Weise es behandelt wird, erfolgt die Kalte Fusion stets nach demselben universellen nuklearen Mechanismus. Begründung: In der Natur existiert in der Regel ein einziger Mechanismus, der verschiedene Phänomene hervorruft.
5. Die Massenenergie wird durch die gleichzeitige Emission von ⁴H sowie von vielen Elektronen in entgegengesetzter Richtung dissipiert. Begründung: Bei der Kalten Fusion ist die Emission von ⁴H und von Elektronen beobachtet worden. Diese Annahme erlaubt die Impulserhaltung im Verlauf der beobachteten Emission, ohne dass sich weitere Annahmen als notwendig erweisen. Da diese Annahme die wichtigste Schlussfolgerung aus der vorliegenden Arbeit beschreibt, handelt es sich solange um eine Annahme, bis diese durch andere Studien überprüft wurde.

4.2 Die Phasen

Wie bereits erwähnt, kommt es nacheinander zu vier separaten Ereignissen, die sich jeweils aus mehreren chemischen Vorgängen zusammensetzen, und denen mehrere nukleare Reaktionen folgen. Jedes dieser Ereignisse muss daher so beschrieben werden, als handele es sich um einen isolierten Mechanismus. Das nukleare Ereignis kann am besten als unerwartete Wirkung einer neuartigen chemischen Anordnung betrachtet werden, an der Elektronen und Wasserstoffkerne beteiligt sind.

Diese Ereignisse treten nicht überall im Material auf, sondern nur an bestimmten einzigartigen Stellen. Im Ergebnis normaler chemischer Prozesse kann es an diesen Stellen zu einer Ansammlung der erforderlichen Atomkerne und Elektronen kommen. Die eigentlichen nuklearen Ereignisse erfolgen nach der Bildung einer solchen Ansammlung, wobei es zu einer kurzen, aber bislang ungeklärten Verzögerung kommen kann.

Zusätzlich zur Fusion kann der nukleare Prozess auch zu sekundären nuklearen Reaktionen führen, die als Transmutationsreaktionen mit den umliegenden Kernen identifiziert werden, oder es können Reaktionen der „Heißen Fusion“ auftreten, wenn die energetische Emission mit den umliegenden Wasserstoffkernen wechselwirkt. Bei diesen seltenen Reaktionen können Strahlung und verschiedene Zerfallsprodukte entstehen, die fälschlicherweise als direktes Ergebnis der Fusionsreaktion selbst angesehen werden können, was zu zusätzlicher Komplexität und Verwirrung führt. Storms und Scanlan berichteten über die Beobachtung von Strahlung, die möglicherweise aus solchen Quellen herrührte. Diese sekundären Kernreaktionen werden hier nicht weiter behandelt. Dennoch muss die gelegentliche Emission von Neutronen in signifikanter Menge im Hinblick auf diese anderen möglichen Reaktionen bewertet werden.

4.2.1 Die Nuklear Aktive Umgebung (NAE)

Die Kalte Fusion setzt eine neuartige Struktur voraus, innerhalb derer sich ein nuklearer Prozess vollziehen kann, ohne dass dafür Energie zugeführt werden muss. Eine Umgebung, in der sich eine derartige Struktur ausbilden kann, findet sich jedoch nur in sehr wenigen Ausnahmefällen. Dennoch wird ein nuklearer Prozess nicht zustande kommen, solange eine solche Umgebung nicht vorhanden ist.

Dieser einzigartige Ort, an dem es zu einer Kernreaktion kommt, wird als Nuklear Aktive Umgebung (NAE - Nuclear Active Environment) bezeichnet. In einem Material bestimmt die Anzahl solcher Orte die maximale Menge an nuklearer Energie, die erzeugt werden kann, da die Anzahl der NAE über die maximale Anzahl an Fusionsstellen entscheidet. Und da die überwiegende Masse des Pd keinerlei NAE aufweist, lässt sich mit dem meisten Pd keine Kalte Fusion erzielen – was bereits mehrfach nachgewiesen wurde. Die Herausforderung besteht also darin, zunächst die NAE zu identifizieren und anschließend Verfahren zu entwickeln, um eine größere Anzahl von ihnen zu produzieren.

Alle möglichen Orte im PdD wurden bereits von irgendjemandem als NAE vorgestellt, darunter die Kristallstruktur selbst, die Leerstellen von D- oder Pd-Atomen, verschiedene Arten von Defekten in der Atomanordnung als auch die Korngrenzen. Auch die Oberfläche kleiner Partikel sowie schmale physikalische Lücken wurden schon als mögliche Orte in Betracht gezogen. Die korrekte Identifizierung der NAE ist von entscheidender Bedeutung, soll die gezielte Schaffung der erforderlichen Umgebung gelingen, soll ein Verständnis für die Funktionsweise der Kalten Fusion erreicht werden und soll daraus letztendlich eine praktikable Energiequelle entwickelt werden. Von daher ist es notwendig, die in Frage kommenden Orte einer kritischen Prüfung zu unterziehen.

Bei der Bewertung einer Stelle auf ihre Eignung hin muss man sich darüber im Klaren sein, dass es bei Weitem nicht ausreicht, zwei D(H)-Kerne einfach nur zur gleichen Zeit am gleichen Ort zu platzieren, um ihre Fusion zu bewirken. Über die D(H)-Kerne hinaus muss es zur Ausbildung einer sehr ungewöhnlichen und komplexen Struktur von Elektronen kommen, die es ermöglicht, die Coulombbarriere so weit herabzusetzen, dass zwischen den Kernen eine Wechselwirkung ausgelöst wird ⁽¹⁾. Sobald sich eine solche Struktur ausgebildet hat, darf diese nicht in Konflikt mit den chemischen Bedingungen an der betreffenden Stelle stehen. Daher muss die Stelle, an der sich die Fusion ereignen können soll, bestimmte chemische Eigenschaften aufweisen, die einen solchen Konflikt ausschließen. Stellen innerhalb der Gitterstruktur, wie beispielsweise Leerstellen, Defekte oder tetraedrische Positionen, würden diese Anforderung verletzen, da sie nach den Regeln zur Bildung einer fcc-Struktur zustande gekommen sind. Auch die Ausbildung einer abweichenden Struktur würde mit diesen Regeln in Konflikt geraten. Diese Feststellung ist von so großer Bedeutung und für Menschen, die die Natur chemischer Wechselwirkungen nicht verstanden haben, so schwer zu akzeptieren, dass ich nur hoffen kann, dass man mir verzeiht, wenn ich die Gründe hierfür auf so viele unterschiedliche Weisen wiedergebe.

(1) Für die Zwecke dieser Diskussion wird vorgeschlagen, dass eine Anordnung von Elektronen notwendig ist, um die Coulombabstoßung zwischen den Wasserstoffkernen zu überwinden. Wenn jedoch andere Methoden zur Erreichung dieses Zieles vorgeschlagen werden, müssen diese ebenfalls mit den hier beschriebenen Beobachtungen und chemischen Anforderungen im Einklang stehen.

Eine tetraedrische Stelle scheitert daran, dass jede dieser Stellen dieselben chemischen Eigenschaften besitzt und daher mit allen anderen tetraedrischen Stellen, die in jeder Pd-Probe vorhanden sind, in chemischer Hinsicht identisch ist. Könnte es an einer dieser Stellen zur Bildung einer NAE kommen, würde sich diese mit gleicher Wahrscheinlichkeit auch an allen anderen Stellen bilden, so dass der Fusionsprozess in allen PdD-Proben sehr häufig auftritt, was so jedoch nicht der Fall ist. Allerdings können die tetraedrischen Stellen kurzzeitig D-Atome enthalten, während sie infolge ihrer Selbstdiffusion an verschiedene Stellen gelangen. Es ist jedoch nicht zu erwarten, dass solche Zufallsereignisse in der Lage sind, einen einzigartigen nuklearen Prozess mit den zu beobachtenden Raten aufrechtzuerhalten.

Aus demselben Grund ist auch die Besetzung von Leerstellen nicht möglich. Im PdD(H) existieren zwei Arten von Leerstellen. Die erste Art bildet sich dort, wo im D(H)-Untergitter Atome fehlen, was zu der beobachteten großen Bandbreite von D(H)/Pd-Verhältnissen führt, da eine variable Anzahl von Leerstellen zufällig durch D⁺- oder H⁺-Ionen besetzt wird. Jede Stelle umfasst nur ein D(H), wobei eine Mehrfachbelegung nur vorübergehend durch die zufällige Bewegung des D(H) infolge der normalen Selbstdiffusion verursacht wird. Wenn diese zufällige Belegung zu LENR führen würde, wäre dieser Effekt erwartungsgemäß sehr viel häufiger und würde in jeder Pd-Probe auftreten, ganz unabhängig von deren Behandlung.

Gelegentlich können Leerstellen von Metallatomen im Pd-Untergitter auftreten, zu deren Entstehung es allerdings unter den Bedingungen, wie sie für LENR zum Einsatz kommen, nur selten kommt. Diese Leerstellen scheiden als NAE aus, denn wenn es sich bei der für die Fusion erforderlichen Atomanordnung in einer Leerstelle um eine chemisch stabile Anordnung handeln würde, dann würde die Leerstelle keine Leerstelle bleiben. Stattdessen würden alle gleichartigen Leerstellen diese stabile Struktur als Teil der normalen Atomanordnung enthalten, wodurch eine andere Atomanordnung ohne Leerstellen gebildet werden würde. Zudem wäre die NAE sehr verbreitet und gleichmäßig über die gesamte Gitterstruktur verteilt, was nachweislich nicht der Fall ist. Darüber hinaus ist die Behauptung von Staker, nach der im PdD Leerstellen existieren, sehr schwach, da die zugrunde liegende Behauptung von Fukai, auf der diese Idee basiert, nicht repliziert werden konnte. Da diese Hohlräume die gleichen chemischen Eigenschaften wie eine Pd-Atomleerstelle besäßen, würde ihre Belegung unter denselben Einschränkungen leiden.

Dadurch verbleiben Risse oder Spalten, die zufällig als Folge des Spannungsabbaus entstanden sind. Da diese Spalten nicht den Anforderungen an eine Kristallstruktur unterliegen, können sie ein breites Spektrum an chemischen Zuständen aufweisen. Da in den Materialien stets Spalten vorhanden sind, während sich LENR nur in seltensten Ausnahmefällen ereignet, dürften sich die erforderlichen Bedingungen in den Spalten nur äußerst selten ausbilden. Dieses Verhalten deutet darauf hin, dass der Spalt über eine kritische Breite und/oder eine kritische chemische Eigenschaft verfügen muss, die nur selten anzutreffen ist. Nur wenn in einem Spalt diese seltene Bedingung gegeben ist, würde sich an dieser Stelle eine chemisch stabile Anordnung von Wasserstoffkernen und Elektronen bilden.

Die Erfahrung hat gezeigt, dass die für die Bildung von NAE erforderlichen Bedingungen im Pd bereits zum Zeitpunkt seiner Herstellung gegeben sein können. Und dieser Zustand bleibt im gesamten Material erhalten, ganz unabhängig von nachfolgenden Behandlungen. Wenn sich also herausstellt, dass ein bestimmtes Stück Pd die Kalte Fusion unterstützt, dann erweisen sich in der Regel auch die meisten Teile der Charge, aus der es stammt, als aktiv. Auch das Gegenteil davon ist zu beobachten. Tote Proben stammen aus Chargen, in denen die allermeisten Proben tot sind. Außerdem hat sich herausgestellt, dass ein sehr reines Pd die Kalte Fusion nicht begünstigt. Stattdessen scheinen bestimmte Verunreinigungen eine wichtige Rolle zu spielen. Dieses Gesamtverhalten schränkt die Eigenschaften der NAE bei der Verwendung von Pd stark ein. Andere aktive Materialien, von denen es viele gibt, würden voraussichtlich andere Eigenschaften aufweisen. Die Herausforderung besteht also darin, eine universelle Eigenschaft zu ermitteln, die sich in allen Materialien schaffen lässt. Ich habe mich mit diesem Problem in einem Artikel befasst, der demnächst im JCMNS veröffentlicht wird. Ein Kopie steht auf LENR-CANR.ORG zum Download zur Verfügung.

4.2.2 Die Nuklear Aktive Struktur (NAS)

Die tatsächliche Anordnung von Atomen und Elektronen, in welcher sich die Fusion ereignet, wird als Nuklear Aktive Struktur (NAS – Nuclear Active Structure) bezeichnet. Diese NAS bildet sich an speziellen Stellen der NAE. Nachdem sich in der NAE eine NAS gebildet hat, kann es mit einer kurzen Verzögerung zur Fusion der NAS kommen. Letztendlich gelangt die Struktur zur „Explosion“, da es hierbei zu einer Umwandlung der Masse in Energie kommt. Anschließend kann sich in derselben NAE erneut eine NAS aufbauen, wenn sich aufs Neue Wasserstoffkerne und Elektronen zusammentun. Dieser Prozess ist in dem von Szpak und seinen Kollegen veröffentlichten Video in Form von blinkenden Hotspots zu erkennen. Die gemessene Leistung ergibt sich aus der Summe jener Energie, welche im Rahmen dieses chaotischen und zufälligen Prozesses im aktiven Material an einer relativ kleinen Anzahl von vereinzelten Stellen freigesetzt wird. Je größer die Anzahl der NAS in jeder NAE und je größer die Anzahl der NAE im Material, umso mehr Energie wird erzeugt. Eine erfolgreiche Erweiterung dieser Energiequelle würde Behandlungsmaßnahmen erfordern, mit deren Hilfe sich sowohl die Anzahl der NAS als auch die Rate erhöhen lässt, mit der sie sich in jedem NAE erneut bilden, nachdem sie durch das jeweilige Fusionsereignis vernichtet wurden. Diese Erkenntnis wird die Konstruktion eines nutzbringenden Energiegenerators maßgeblich beeinflussen.

4.2.3 Der Unterschied zwischen der Heißen Fusion und der Kalten Fusion

Um eine Erklärung für die Kalte Fusion zu finden, hat man sich zunächst ganz auf das Verhalten der Heißen Fusion fokussiert. Aus den nachfolgend aufgeführten Gründen führt dies jedoch in die Irre.

Bei der Heißen Fusion wird die Coulombbarriere dadurch überwunden, dass man sich für das Zusammenstoßen der Atomkerne der kinetischen Energie bedient – üblicherweise in einem sehr heißen Plasma. Wird die Heiße Fusion stattdessen in einem Material mittels kinetischer Energie auf dem Wege des Ionenbeschusses ausgelöst, so zerfällt das resultierende Kernreaktionsprodukt in zwei unterschiedliche Paare von Kernreaktionsprodukten, so wie in Abbildung 22 dargestellt, mit nahezu gleicher Wahrscheinlichkeit, selbst wenn nur die geringste Menge an Energie aufgewendet wird. Die im Material vorhandenen Elektronen können eine lokale Abschirmung bewirken, wodurch sich die sehr niedrige Rate der Heißen Fusion gegenüber der im Plasma verursachten Rate erhöht, bei der eine solche Abschirmung nicht existiert (siehe Abbildung 23). In diesem Fall verringern die Elektronen nahe der Stelle jeder zufälligen Begegnung geringfügig die Höhe der lokalen Barriere, wobei die Höhe der Abschirmung mit sinkender Annäherungsgeschwindigkeit zunimmt, weil der Abschirmung mehr Zeit für ihre Wirkung zur Verfügung steht. Dieser Abschirmungseffekt reicht jedoch nie aus, um die verringerte Reaktionsgeschwindigkeit zu kompensieren, wie sie durch die Verringerung der kinetischen Energie verursacht wird. Dieses Verhalten zeigt bestenfalls, dass in einer chemischen Struktur im Verlauf der Heißen Fusion eine Elektronenabschirmung möglich ist. Im Vergleich fällt diese Art der Abschirmung bei der Kalten Fusion wesentlich stärker aus, da die Kerne hier für längere Zeit in engem Kontakt miteinander stehen können.

Abbildung 22: Emissionsenergie bei der Heißen Fusion von Deuteronen nach Czerski. Die Emission von ⁴He und einer Gammastrahlung ist sehr unwahrscheinlich und tritt bei der Kalten Fusion nicht auf.

Abbildung 23. Das Ergebnis des D⁺-Beschusses von Ti mit der angegebenen kinetischen Energie, um die Rate der Heißen Fusion im Verhältnis zu derjenigen zu erzeugen, die bei einer kinetischen Energie von 2,45 KeV angewendet wird. Ein berechneter Wert für das Abschirmungspotenzial (U_e) ist dargestellt. Der ungeschirmte Wirkungsquerschnitt wird erzielt, wenn die Fusion im Plasma stattfindet. Die absolute Fusionsrate bei dieser Energie liegt nahe der Nachweisgrenze, zu der die Elektronenabschirmung nur eine sehr geringe zusätzliche Rate beiträgt.

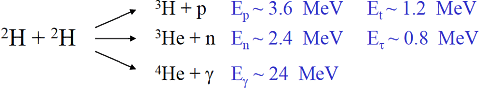
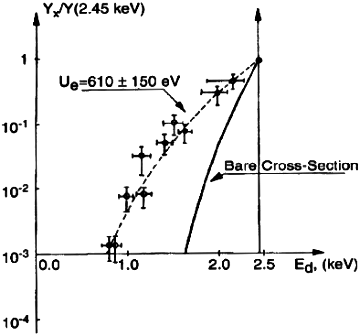
Bei der Kalten Fusion muss es in der Nähe der Wasserstoffkerne zunächst zu einer ausreichenden Konzentration von Elektronen kommen, um das Coulombfeld zu verringern. Leider gibt es hier ein Problem, denn es ist nicht belegt, dass sich Elektronen auf diese Weise konzentrieren. Selbst wenn sich Elektronen zu chemischen Verbindungen oder Kristallen zusammenschließen, hält die Elektronenstruktur die Kerne weit voneinander entfernt. Damit es zu einer Kalten Fusion kommen kann, müssen die Elektronen ihren Abstand zueinander verringern. Dies erfordert allerdings anstelle einer Variation des Mechanismus der Heißen Fusion eine ganz neue Art von Elektronenwechselwirkung. Diese Erkenntnis bildet eine der wichtigsten Schlussfolgerungen aus dieser Entdeckung.

Das ⁴H und alle übrigen Kernreaktionsprodukte werden bei der Kalten Fusion jedoch mit ausreichend kinetischer Energie emittiert, um eine Heiße Fusion auslösen zu können, sofern sie in der sie umgebenden Struktur auf D oder H treffen, wodurch es zu einem Nebeneinander von Reaktionsprodukten aus Kalter und Heißer Fusion kommt. Wenn diese Mischung nicht korrekt bewertet wird, kann dies zu Fehlinterpretationen führen. Die Vermutung, nach der eine Fraktofusion die Ursache für die gelegentlich auftretende energiereiche Strahlung bildet, sollte diese vielmehr in der Kalten Fusion begründet sehen. In diesem Fall wäre der kurzzeitige Prozess der Kalten Fusion, welcher zu der leicht nachweisbaren energiereichen Strahlung führt, zu schwach, um seine einzigartige Signatur erfassen zu können.

4.3 Die nuklearen Reaktionsprodukte

Ausgehend von den in Abbildung 8 zusammengefassten Daten stellt ⁴He das hauptsächliche nukleare Reaktionsprodukt dar, auf das die gemessene Energie zurückzuführen ist. Storms und Scanlan haben aufgezeigt, dass Helium, so wie in Abschnitt 3.8.1 beschrieben, nicht direkt dem nuklearen Ereignis entspringt. Stattdessen wird ein Wasserstoffisotop emittiert. Gleichwohl reichert sich bei der Erzeugung von Kernenergie in der Umgebung ⁴He-Gas an. Wie können diese beiden Tatsachen miteinander in Einklang gebracht werden?

Bei ⁴H handelt es sich um das einzige Wasserstoffisotop, das in der Lage ist, in ⁴He zu zerfallen. Allerdings wird diesem Isotop auch nachgesagt, dass es durch die Emission von Neutronen schnell zerfällt, sofern es mit hoher Energie erzeugt wird. Da diese Schlussfolgerung dazu dient, die hier aufgestellte Behauptung zu widerlegen, müssen die Zerfallseigenschaften von ⁴H untersucht werden, insbesondere im Hinblick auf die in Abbildung 15 dargestellten Messungen sowie auf die Möglichkeit, dass es zu einer Veränderung des Zerfallsmodus kommt, wenn die Erzeugung des Isotops bei niedriger Energie erfolgt. Immerhin ändert sich der Zerfallsmodus des aus der D+D-Fusion resultierenden nuklearen Reaktionsproduktes, sobald es sich um eine für die Kalte Fusion typische Energiezufuhr handelt, so wie in Abschnitt 4.2.3 beschrieben.

4.3.1 Der Zerfallsmodus des ⁴H

In diesem Aufsatz geht es nicht darum, die Existenz von ⁴H zu bewerten, was bereits an anderer Stelle erfolgt ist, so dass ich hier nur einige Überlegungen anstellen möchte, die es wert sind, in der Zukunft näher untersucht zu werden. Für den Anfang sollen ein paar grundlegende Beobachtungen beschrieben werden.

Es wird davon ausgegangen, dass es zu einer kurzzeitigen Bildung eines ⁴H-Kerns kommt, wenn flüssiges Deuterium mit ³H⁺-Ionen beschossen wird, welche über eine Energie von 57,5 MeV verfügen. Dabei wurden Emissionen von energiereichen p, n und ³H beobachtet. Man vermutet, dass das ⁴H entsteht, wenn das Deuteron ein Neutron auf das ³H überträgt, wodurch ein energiereiches p emittiert wird. Das ⁴H stößt das Neutron dann schnell wieder ab, woraufhin das ³H und das Neutron in entgegengesetzte Richtungen emittiert werden. Ich gehe davon aus, dass die Beobachtungen, die der Annahme der Bildung von ⁴H zugrunde liegen, auch durch die Aufspaltung eines Deuterons in p und n erklärt werden könnten, ohne dass dabei ⁴H entsteht. Die zahlreichen Berechnungen des Energiezustandes von ⁴H basieren auf diesen und ähnlichen Beobachtungen bei Anwendung hoher Energien. Noch unbekannt ist, ob ein stabiler Energiezustand verfügbar ist, wenn das Isotop bei niedriger Energie und in Anwesenheit einer Elektronenwolke erzeugt wird.

4.3.2 Die Folgen der Bildung von ⁴H

Wie kann es dazu kommen, dass anstelle von ⁴He die Bildung von ⁴H erfolgt, obwohl in der Umgebung doch Helium vorhanden ist? Diese Frage muss mit einer weiteren Frage verbunden werden. Wie kann ³H (Tritium) durch denselben Mechanismus erzeugt werden wie ⁴H, um der Annahme Nr. 3 gerecht zu werden?

Wie in der vorangegangenen Beschreibung bereits erwähnt, erfordert die Herabsetzung der Coulombbarriere in der NAS eine Ansammlung von Elektronen. Nachdem sich die Elektronen um die Wasserstoffkerne angesammelt haben, würden sie miteinander und mit den Kernzuständen der Wasserstoffkerne wechselwirken. Nehmen wir an, dass während dieses Prozesses eines dieser Elektronen vom nuklearen Reaktionsprodukt eingefangen wird, wodurch ⁴H gebildet wird, wie in Tabelle 1 in der ersten Reaktion beschrieben. Auch Godes hat die Bildung dieses nuklearen Reaktionsproduktes vermutet, allerdings über einen Mechanismus, der die direkte Bildung eines Neutrons einschließt. Obwohl es bei dem hier vorgestellten Mechanismus zur Bildung eines Neutrons kommt, erfolgt diese Bildung im nuklearen Reaktionsprodukt, von dem die erforderliche Energie geliefert wird, so dass keine Energie aus der Umgebung in Höhe von 0,78 MeV zugeführt werden muss, wie es bei der direkten Bildung eines Neutrons aus p⁺ und e^- im freien Raum erforderlich ist. Die Frage lautet: „Ist dieser Mechanismus in der Lage, auch alle anderen bekannten nuklearen Reaktionsprodukte zu erzeugen, ohne dass zusätzliche Annahmen getroffen werden müssen?“

Die anderen in Tabelle 1 aufgeführten Reaktionen ergeben sich aus der Anwendung der Annahmen Nr. 3 und Nr. 4. Auf diese Weise lässt sich die Bildung von Tritium aus der Fusion von H⁺ und D⁺ samt einem eingefangenen Elektron erklären. Eine ähnliche Reaktion zwischen zwei H⁺ würde zu einem energiereichen Deuteron führen, begleitet von der gleichen energiereichen Elektronenemission. Zusammengenommen erscheint der gesamte Prozess der Umwandlung eines Wasserstoffisotops in ein anderes als das Ergebnis einer Fusion unter Beteiligung von Elektronenabschirmung und Elektroneneinfang.

Eine geringe Verunreinigung von normalem Wasserstoff mit D würde zwar einen kleinen Beitrag zur Fusion D + e + H leisten, wäre aber zu gering, um die festgestellte Menge an Tritium zu erklären. Auch die bei normalem Wasserstoff beobachtete Energiemenge lässt sich nicht durch die Fusion zwischen einzelnen D-Kernen erklären. Ebenso würde eine geringe Menge an H in gereinigtem D zu keinem nachweisbaren Ergebnis führen. Somit muss nach anderen Erklärungen gesucht werden.

Tabelle 1. Vorgeschlagene Reaktanten, nukleare Reaktionsprodukte und Energie für jede durch die Kalte Fusion hervorgerufene Reaktion

(D + e + D) = 4H = 4He + e (schneller Zerfall) + ν	23,8 MeV
(H + e + D) = 3H = 3He + e (langsamer Zerfall) + ν	4,9 MeV
(H + e + H) = 2H (stabil)	1,9 MeV
(T + e + D) = 4H + n = 4He + e (schneller Zerfall) + ν	< 19 MeV
(T + e + H) = 4H = 4He + e (schneller Zerfall) + ν	< 21 MeV

Alle anfänglichen nuklearen Reaktionsprodukte werden begleitet durch die Emission zahlreicher Elektronen.

Wird ausschließlich H zur Fusion gebracht, ohne dass die NAE anfänglich D enthält, würde die Menge an Tritium (³H) langsam ansteigen, da sich im Material das erste nukleare Reaktionsprodukt (D) ansammelt und mit dem H fusioniert. Steigt die Konzentration von D weiter an, würde die D+D-Reaktion das ⁴H und dessen Zerfallsprodukt ⁴He erzeugen. Daher würde man dieselbe nukleare Emission sowohl bei der Verwendung von reinem H als auch von D beobachten, so wie dies von Storms und Scanlan beschrieben wurde. Die Menge an Energie, die aus dieser komplexen Ansammlung von Reaktionen resultiert, wäre zwar geringer als bei der Verwendung von reinem D + e + D, aber dennoch signifikant.

Warum aber scheint Ni erforderlich zu sein, um signifikante Mengen an Energie zu erzeugen, wenn ausschließlich H zum Einsatz kommt? Ich vermute, dass das entstehende D und Tritium in der NAE von Ni im Vergleich zu Pd effektiver gebunden wird, so dass diese als Reaktanten eine größere Effektivität aufweisen. Infolgedessen wäre die Energiemenge größer und die Menge an nachgewiesenem Tritium geringer als bei der Verwendung von Pd, da die hauptsächlichen energieerzeugenden Reaktionen (D + e + D und D + e + T) im Pd mit geringerer Wahrscheinlichkeit ablaufen, weil die nuklearen Reaktionsprodukte rasch aus dem aktiven Zentrum herausdiffundieren.

Die wenigen Neutronen, die bei der Bildung von Tritium festgestellt werden, resultieren aus der Fusion zwischen den Tritium- und den Deuteriumkernen. Die große Streuung der T/n-Werte (Abbildung 11) ist auf zufällige Schwankungen bei den Konzentrationen von D und T im Laufe der verschiedenen Versuche zurückzuführen. Eine sorgfältige Analyse der Veränderungen im T/n-Verhältnis, während gleichzeitig die Konzentrationen von T und D variiert werden, könnte die wahre Herkunft der Neutronenemission aufzeigen.

Das in Abbildung 8 dargestellte widersprüchliche Verhalten lässt sich nun erklären. Anstatt dass das Helium nach seiner Entstehung im Wesentlichen eingeschlossen bleibt, handelt es sich bei dem nuklearen Reaktionsprodukt um ein Wasserstoffisotop mit der Fähigkeit, schnell aus dem Material herauszudiffundieren. Ein variabler Anteil des ⁴H könnte zu ⁴He zerfallen, noch bevor es aus dem Material herausdiffundieren kann. Folglich ergibt sich die im PdD zurückgehaltene Menge aus dem Verhältnis zwischen der Diffusionsrate des ⁴H und seiner Zerfallsrate und nicht allein aus der Position, an der die Fusionsreaktion im Material stattgefunden hat.

Darüber hinaus bedürfen zwei weitere Fragen einer Klärung: Auf welche Weise wird der Impuls erhalten, und wo ist die Fusionsenergie, die dem emittierten ⁴H fehlt?

4.3.3 Implikationen der angenommenen Elektronenemission

Auf der Suche nach dem Mechanismus, über den die freigesetzte Kernenergie dissipiert wird, wurden zahlreiche Vorschläge unterbreitet. Für die hier angestellten Betrachtungen gehen wir davon aus, dass diese Energie auf dem Wege der Emission von Elektronen disipiert wird, so wie dies als Elektronenstrom im LEC festgestellt wurde. (Annahme Nr. 5) Denn wäre hier zur Abschirmung der Coulombbarriere eine Anordnung von Elektronen erforderlich, müsste man erwarten, dass diese Elektronen den gleichen Energiezustand aufweisen wie die sich zusammenschließenden Kerne. Damit stünden sie zur Verfügung, um diese Energie in Form von Elektronenemissionen zu dissipieren. Welche Implikationen ergeben sich nun aus dieser Annahme?

Durch eine Kombination der Impulserhaltungsgleichung mit der bereits bekannten kinetischen Energie des ⁴H und der durch die Fusion freigesetzten Gesamtenergie lässt sich die Anzahl der emittierten Elektronen nebst deren Energie berechnen. Die folgenden Gleichungen beschreiben die Bedingungen, die erforderlich sind, um die Impulserhaltung durch die Emission von ⁴H in die eine Richtung sowie aller an der Entstehung von ⁴H beteiligten Elektronen in die entgegengesetzte Richtung zu gewährleisten.

A * M_e * V_e = M_h * V_h, wobei A für die Anzahl der Elektronen steht, die für jedes emittierte ⁴H emittiert werden, M_e für die Masse eines Elektrons, V_e für die Durchschnittsgeschwindigkeit der emittierten Elektronen, M_h für die Masse des ⁴H und V_h für die Geschwindigkeit des ⁴H, das in der den Elektronen entgegengesetzten Richtung emittiert wird.

K_e = ½ * A * M_e * V_e² = gesamte kinetische Energie der emittierten Elektronen = (23.84 - K_h) x 10⁶ eV
K_h = ½ *M_h * V_h² = kinetische Energie von ⁴H (Werte aus Abbildung 15)

M_h = Masse He + Masse e = 4.002603 + 0.000548 = 4.003251 amu

Diese Masse stellt die untere Grenze dar, da ein kleiner Teil der Masse bei der Emission des Elektrons und des Antineutrinos im Zuge der Entstehung von ⁴He auf dem Wege des Betazerfalls von ⁴H als Energie verloren geht.

Diese Gleichungen lassen sich wie folgt reduzieren:

A = (4,003251 * K_h)/(0,000548 * (23,84 - K_h)) = Gesamtzahl der mit jedem ⁴H, das über eine gemessene kinetische Energie von K_h verfügt, emittierten Elektronen

(23,84 - K_h) ∙ 10⁶ / A = Energie jedes emittierten Elektrons

Die Werte von K_h werden für jeden Energiespitzenwert aus den Werten von K-K abgeleitet, wie dies durch die Methode der kleinsten Quadrate beschrieben und in Abbildung 15 dargestellt wird. Die Wahl ist auf diese Werte gefallen, da sie näher an der tatsächlich emittierten Energie zu liegen scheinen als die Werte von S-S. Die berechneten Werte für die kinetische Energie jedes Elektrons sowie die Anzahl der bei jeder Fusionsreaktion emittierten Elektronen (A) sind in Abbildung 24 dargestellt. Da das nukleare Reaktionsprodukt in diskreten Schüben und mit diskreter Energie emittiert wird, werden auch die Elektronen auf ähnliche Weise emittiert, jedoch in umgekehrter Größenordnung und in entgegengesetzter Richtung.

Wie die Abbildungen 13 und 16 belegen, zeigt sich beim emittierten ⁴H mit der niedrigsten Energie im Vergleich zu den anderen Ionenemissionen der größte Fluss. Abbildung 24 zeigt, dass zugleich auch der geringste Fluss an Elektronen emittiert wird, allerdings mit der im Vergleich zu allen anderen Elektronen höchsten Energie. Darüber hinaus sind alle Peaks der ⁴H-Emissionen durch eine gleiche Menge an kinetischer Energie voneinander getrennt, und ebenso alle Peaks durch eine gleiche Anzahl von emittierten Elektronen. Dieses außergewöhnliche Verhalten weist mehrere Implikationen auf.

Abbildung 24. Die Anzahl der Elektronen und deren Energie, die mit jedem ⁴H emittiert werden, um die Fusionsenergie abzuleiten, während der Impuls erhalten bleibt. Die Werte wurden unter Verwendung der in Abbildung 15 angegebenen Gleichung für die ⁴H-Energie basierend auf den Werten von K-K ermittelt.

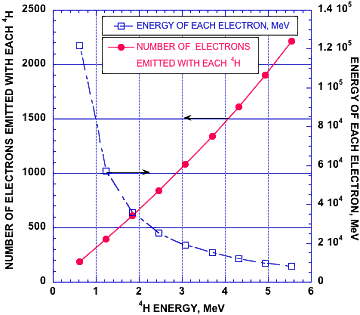
Um die Impulserhaltung zu gewährleisten, müssen sich alle emittierten Elektronen in dieselbe Richtung bewegen und dabei in entgegengesetzter Richtung zur jeweiligen ⁴H-Emission. Das erfordert, dass die Elektronen einen eng fokussierten Strahl bilden. Ganz unabhängig von ihrer Energie könnten nur solche Ionen detektiert werden, die sich in eine bestimmte Richtung bewegen. Diese Anforderung legt nahe, dass der Spalt, aus dem all die erfassten Ionen stammen, keine symmetrische Form hat, sondern eine bevorzugte Richtung aufweist.

Da jeder ⁴H-Peak von seinem benachbarten Peak durch eine gleiche Anzahl von emittierten Elektronen (216) und durch den gleichen Betrag an kinetischer Energie (0,617 MeV) getrennt ist, deutet dies darauf hin, dass in der Anordnung, wie sie sich nach der Fusion zeigt, ein regelmäßiges Array von Energieniveaus existiert, die voneinander durch dieselbe Anzahl von Elektronen getrennt sind. Diese Werte weisen eine unbekannte Unsicherheit auf, da das ⁴H auf seinem Weg durch das Material Energie verliert.

Die Existenz mehrerer Energieniveaus, von denen jedes eine unterschiedliche Wahrscheinlichkeit für seine Bildung aufweist, legt nahe, dass es beim Zerfall eines jeden Energieniveaus zu einer Verzögerung kommt, sodass zusätzliche Elektronen Zeit haben, sich anzusammeln. Dadurch kann das nächste instabile Niveau mit einer größeren Anzahl von Elektronen, aber mit verringerter Wahrscheinlichkeit gebildet werden. Infolgedessen wird eine relativ größere Anzahl von Elektronen emittiert, wobei jedes einzelne weniger Energie aufweist, da jedes Energieniveau besetzt wird und sich dann langsam zersetzt. Es handelt sich hier um einen einzigartiger Prozess, der noch weiter untersucht werden muss.

Es wird angenommen, dass diese Elektronen die beobachtete Photonenstrahlung in Form von Bremsstrahlung erzeugen. Die von Swartz und Verner gelieferte Erklärung dieses Prozesses trifft jedoch nicht zu. Stattdessen werden die von jeder NAE ausgehenden Elektronenstrahlen in zufällige Richtungen emittiert. Während diese Strahlen das umgebende Material durchqueren, würde deren Energie in Photonenstrahlung umgewandelt werden. Diese Photonen würden sich in die gleiche Richtung wie die Elektronenstrahlen bewegen und könnten zu den in Abbildung 17 gezeigten Photonenstrahlen führen. Da die Elektronen ein breites Energiespektrum aufweisen, würden auch die resultierenden Photonen ein entsprechend breites Spektrum zeigen, wie es bereits beobachtet wurde.

In Abbildung 25 ist das resultierende Elektronenspektrum dargestellt, wobei die relative Intensität in Abhängigkeit von der Energie der Elektronen aufgetragen ist, wenn diese zusammen mit dem entsprechenden ⁴H emittiert werden. Dieses Spektrum entsteht, indem die Intensität der mit jedem ⁴H-Ion emittierten Elektronen, wie in Abbildung 22 gezeigt, durch die Gesamtzahl aller Elektronen für diesen Energiebereich der ⁴H-Ionen dividiert wird. Das Ergebnis ist ein hypothetisches und idealisiertes Elektronenspektrum. Die durchschnittliche Energie der emittierten Elektronen liegt bei etwa 0,03 MeV, wobei die meisten Elektronen eine Energie zwischen 0,01 und 0,02 MeV aufweisen. Folglich würde diese Emission ein entsprechendes Magnetfeld erzeugen und von diesem beeinflusst werden.

Abbildung 25. Das errechnete Spektrum der Elektronenenergie, bevor die emittierten Elektronen ein Material durchdrungen haben. Der Anteil des gesamten Elektronenemissionsflusses ist für jeden ⁴H-Peak mit einer Energie von unter 6 MeV dargestellt, so wie von K-K berichtet. Es wird erwartet, dass dieses Spektrum der Elektronenemissionen zum gleichen Zeitpunkt erscheint, zu dem auch die ⁴H-Ionen emittiert werden.

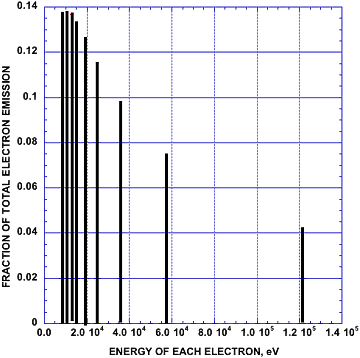
4.3.4. Die Implikationen der Notwendigkeit eines Zusammenschlusses von Elektronen

Da die Bildung einer NAS es erfordert, dass sich sowohl Atomkerne als auch Elektronen am selben Ort zusammenschließen, würde die Zuflussrate, mit der beide jeweils zur NAS gelangen können, die Energiemenge bestimmen. Dieser Prozess benötigt Zeit und reagiert empfindlich auf jene Größen, die die Verfügbarkeit von Kernen und Elektronen für die anwachsende NAS erhöhen. Die Verfügbarkeit von Kernen für die NAS ergibt sich hauptsächlich aus der Temperatur und dem Zufluss von Wasserstoffkernen, wie dies bereits beschrieben wurde. Jetzt werde ich mich den Auswirkungen zuwenden, die die Verfügbarkeit von Elektronen mit sich bringt.

Elektronen in einem metallischen Leiter, wie etwa PdD, sind auf zwei unterschiedliche Weisen verfügbar. Die Elektronen, welche die Atome in einer Kristallstruktur miteinander verbinden, sind stark gebunden und somit nicht verfügbar. Im Gegensatz dazu sind die Leitungselektronen frei beweglich und können von den NAS eingefangen werden. Das Anlegen einer Spannung, welche die Leitungselektronen in Bewegung versetzt, würde die Wahrscheinlichkeit erhöhen, dass ein solches Elektron auf eine NAE trifft und von dieser eingefangen wird. Dieser zu erwartende Effekt ist in Abbildung 6 dargestellt, wo verschiedene Ströme bei unterschiedlichen Temperaturen angelegt werden. Die Temperatur hat nur einen geringen Einfluss auf den Effekt des Stroms. Im Gegensatz dazu wirkt sich eine Erhöhung der Stromstärke in zunehmendem Maße auf die Reaktionsrate aus, wie dies zu erwarten wäre, wenn der NAS eine große Anzahl von Elektronen zugeführt werden muss.

Es wäre zu erwarten, dass ein Magnetfeld den Effekt des Stroms verstärkt, da sich die Weglänge der Elektronen durch ihre Rotation um die magnetischen Kraftlinien vergrößert, wodurch sich die Wahrscheinlichkeit eines Zusammentreffens mit einer NAS erhöht.

Dieser Strom würde außerdem bewirken, dass D- oder H-Ionen im Material wandern und sich aufgrund der Elektromigration, die häufig als Coehn-Effekt bezeichnet wird, in der Nähe der negativen Polarität konzentrieren, was die Verfügbarkeit von Atomkernen weiter erhöht.

Untermauert wird dieser vermutete Mechanismus durch Godes, Celani und Kollegen sowie Staker, die durch das Anlegen eines Stroms die Energieerzeugung erfolgreich steigern konnten. Allerdings erklären sie diesen Erfolg durch unterschiedliche Mechanismen. Die Herausforderung besteht darin zu bestimmen, welcher der vorgeschlagenen Mechanismen korrekt ist.

4.3.5 Vorhersagen

Die Zusammenstellung der Verhaltensweisen ermöglicht es, mehrere überprüfbare Vorhersagen zu treffen. Diese Vorhersagen können zur Bestätigung der Erklärung herangezogen werden sowie als Orientierung für zukünftige Studien dienen.

1. Bei der Verwendung von D, das kein H enthält, wird kein Tritium erzeugt.
2. Bei der Verwendung von gewöhnlichem H, das kein zusätzliches D enthält, wird schließlich mit zunehmender Rate Tritium erzeugt, da die Menge an D infolge der anfänglichen Fusionsreaktion ansteigt. Der Neutronenfluss wird ebenfalls zunehmen, da die Rate der Fusion von Tritium und Deuterium steigt. Eine Mischung aus D und H wird Tritium am schnellsten erzeugen.
3. Die Verwendung entweder von D oder von H wird Kernenergie erzeugen, wobei H weniger Energie liefert als D, wenn die gleiche Anzahl von NAS vorhanden ist.
4. Die Verwendung entweder von D oder von H wird zur Emission von ⁴H und durch schnellen Betazerfall zur Bildung von ⁴He führen, dem Zerfallsprodukt von ⁴H. Die Verwendung von gewöhnlichem H wird ein größeres, aber variables Verhältnis von He/Energie im Vergleich zu D erzeugen.
5. Ein durch die NAE geleiteter Elektronenstrom wird die Fusionsrate erhöhen.
6. Ein Fluss von Wasserstoffisotopen durch die NAE wird die Fusionsrate erhöhen.
7. Die Verwendung entweder von D oder von H wird einen Fluss von emittierten Elektronen in unterschiedlicher Menge und mit unterschiedlicher Energie erzeugen.
8. Die NAE kann durch Nanobearbeitung eines leitfähigen Metalls erzeugt werden, auf das eine geeignete Quelle für Deuterium, ein elektrischer Strom und erhöhte Temperatur angewendet werden.
9. Die gesamte Strahlung, bestehend aus Photonen, Ionen und Elektronen, wird als stark fokussierte Strahlen in zufällige Richtungen mit einem komplexen Energiespektrum emittiert.
10. Der Großteil der Kernenergie wird durch eine große Anzahl von Elektronen abgeführt, wobei jedes nur einen kleinen Bruchteil der Gesamtenergie trägt und in einem kohärenten Zusammenhang mit den anderen Elektronen steht.
11. Der Fusionsprozess umfasst eine Abfolge gleichmäßig verteilter Energiezustände, die mit einer kurzen Halbwertszeit zerfallen und ihre Energie als kinetische Energie vieler Elektronen einerseits und des nuklearen Reaktionsprodukts andererseits freisetzen, die beide jeweils in entgegengesetzte Richtungen strahlen.
12. Gelegentlich werden Reaktionsprodukte beobachtet, die durch den heißen Fusionsmechanismus entstehen, insbesondere wenn die D-Konzentration hoch ist.

5.0 Diskussion des Nuklearprozesses

Da die Bedingungen, die erforderlich sind, um eine Kalte Fusion zu bewirken, für die Kernphysik einzigartig sind, war es sehr schwierig, diesen Prozess zu akzeptieren und zu verstehen. Es wurden mittlerweile jedoch genügend Beweise zusammengetragen, um zu zeigen, dass es sich bei der Kalten Fusion um ein reales Phänomen und nicht um einen Irrtum handelt. Der nächste Schritt besteht darin, diese Beweise zu einer nützlichen Beschreibung dessen, wie der Prozess funktioniert, zusammenzufügen und dieses Verständnis auf die Schaffung einer praktischen Energiequelle anzuwenden. Um dieses Ziel zu erreichen, müssen die entscheidenden Messungen mit größerer Präzision durchgeführt und die vorgeschlagenen Vorhersagen unvoreingenommen getestet werden. Nur dann wäre eine mathematische Beschreibung des Warum des nuklearen Mechanismus von Nutzen. Dieses notwendige Ziel wird derzeit durch das Fehlen allgemein anerkannter, verlässlicher Beobachtungen behindert. Diese Abhandlung wird als Leitfaden zur Verfügung gestellt, um zu zeigen, wie solche Informationen erlangt werden könnten und wie das derzeitige Wissen durch eine logische Beziehung erklärt werden kann, die ich als Modell mit Vorhersagen vorschlage, anhand derer es überprüft werden kann.

Die Kalte Fusion erzeugt ⁴He als nukleares Reaktionsprodukt, aus dem der Großteil der beobachteten Energie stammt. Dieses Nuklid fragmentiert nicht, wenn es in einer chemischen Umgebung erzeugt wird, im Gegensatz zu seinem Verhalten, wenn es durch die Anwendung ausreichender kinetischer Energie entsteht. Was verursacht diese kontrastierenden Verhaltensweisen?

Die zweite Frage betrifft die Art und Weise, wie die Coulombbarriere reduziert wird, ohne dass kinetische Energie aufgebracht werden muss. Wie in den vorangegangenen Abschnitten beschrieben, wird davon ausgegangen, dass dieser Prozess durch eine Anordnung von Elektronen zustande kommt.

Diejenigen Elektronen, die mit den Kernenergiezuständen interagierten, um die Coulombbarriere zu senken, wären in der Lage, einen Teil der Massenänderung als Energie abzugeben, wenn sie nach dem Fusionsprozess aus der Anordnung emittiert werden, nachdem Massenenergie freigesetzt wurde. Diese Emission könnte als eine nukleare Explosion betrachtet werden, die die umliegenden Elektronen in entgegengesetzte Richtungen zum nuklearen Reaktionsprodukt aussendet. Wenn die letzten Elektronen emittiert werden, könnte eines von ihnen von dem finalen Kernenergiezustand eingefangen werden, um ⁴H zu bilden. Dadurch kann angenommen werden, dass dieses finale nukleare Reaktionsprodukt nicht fragmentiert, da die Überschussenergie in Form von Betastrahlung freigesetzt werden könnte.

Lassen Sie uns nun tiefer in den Kaninchenbau einsteigen. Wurde eine derartige Elektronenanordnung schon einmal in Betracht gezogen? Mills lieferte eine teilweise Beschreibung dieses Prozesses in Form des Hydrinos. Rathke und Meulenberg ergänzen das Verständnis darüber, wie ein Elektron oder möglicherweise viele Elektronen einen Zustand direkter energetischer Interaktion mit dem Kern selbst erreichen könnten, um weitere Details. Die daraus resultierende Struktur könnte als ein großer Kern betrachtet werden, der Elektronen in Energieniveaus enthält, die normalerweise weder im Kern noch in normalen chemischen Energieniveaus vorkommen. Wurde eine solche Struktur schon einmal beobachtet?

Wie von Shoulders beschrieben, weist die von ihm entdeckte Struktur die erforderlichen Eigenschaften auf, allerdings erfuhr sie keine Fusion, als er sie in Luft erzeugte. Möglicherweise unterstützte die Struktur die Fusion nicht, weil sie kein Wasserstoffisotop enthielt. Er nannte diese Struktur, die viele Elektronen und wenige Kerne enthält, EVO. Fox und Jin erforschten diese Idee ausführlicher.

Rambaut beschreibt diese Elektronenstruktur als magnetischen Monopol. Hubler bietet eine andere Erklärung für dasselbe Verhalten. Kugelblitze haben eine ähnliche Eigenschaft, jedoch in größerem Maßstab. Da diese Struktur in ihren verschiedenen Formen durch elektrische Entladungen in einem Gas erzeugt und untersucht wurde, muss ihre Fähigkeit, sich auch in einem festen chemischen Umfeld zu bilden, angenommen werden.

Dieser langsame Fusionsprozess wäre einzigartig und bisher nicht beobachtet worden, da alle bisherigen Kernreaktionen kinetische Energie involvierten, die die schnelle Freisetzung nuklearer Energie in Form energiereicher nuklearer Reaktionsprodukte oder langsamer in Form radioaktiven Zerfalls durch einen anderen Mechanismus erzwingen würde. Radioaktiver Zerfall tritt bei der Kalten Fusion nur selten auf, da die gesamte Energie durch die Elektronenemission freigesetzt wird, außer bei der Bildung von ⁴H und ³H. Die verbleibende Energie, die durch den Betazerfall freigesetzt wird, wäre im Vergleich zur anfänglichen Freisetzung gering, was die Menge der verlorenen Energie durch das resultierende Neutrino begrenzt. Die häufig beobachteten Transmutationsreaktionen werden durch die kinetische Energie der Fusionsreaktion ermöglicht, was erklärt, wie die gigantische Coulombbarriere überwunden werden kann. Ein Teil der beobachteten Strahlung könnte entstehen, wenn die Transmutationsprodukte radioaktiven Zerfall erfahren oder wenn lokale Heiße Fusion infolge der Emission von Reaktionsprodukten der Kalten Fusion auftritt.

6.0 Zusammenfassung

Normalerweise interagieren die chemischen Energieniveaus nicht auf direktem Wege mit den nuklearen Energieniveaus. Das bedeutet, dass eine Bedingung geschaffen werden muss, die in einer normalen chemischen Struktur so nicht vorhanden ist, bevor es zu einer Fusion kommen kann. Es wird vorgeschlagen, dass diese einzigartige Struktur nur in physikalischen Spalten mit einer kritischen Größe im Nanometerbereich entsteht. Diese Spalten können durch viele verschiedene Vorbehandlungen und in vielen verschiedenen Materialarten erzeugt werden, einschließlich durch Nanobearbeitung.

Die vorgeschlagene Fusionsstruktur besteht aus zwei Kernen eines beliebigen Wasserstoffisotops und einer Vielzahl von Elektronen. Um eine Fusion zu bewirken, muss diese Struktur dazu führen, dass sich mindestens zwei Kerne einander so stark annähern, dass ihre Kernenergiezustände miteinander wechselwirken können. Diese Verringerung des Abstandes, die als Abschirmung oder Tunneleffekt bezeichnet werden kann, wird durch die Anordnung vieler Elektronen verursacht, die miteinander und mit den Kernen einen ungewöhnlichen Energiezustand bilden. Der Entstehungsprozess muss den Regeln entsprechen, die für chemische Prozesse gelten, da anfangs keine Kernwechselwirkungen erwartet werden. Das bedeutet, dass der Entstehungsprozess exotherm sein muss, da seine Bildung sonst nicht spontan wäre und nicht den Anforderungen des Zweiten Hauptsatzes der Thermodynamik entsprechen würde. Diese Erkenntnis lenkt die Aufmerksamkeit auf eine neue Art von Elektronenwechselwirkung, die in der Lage ist, die gegenseitige Abstoßung aufgrund ihrer Ladung zu kompensieren. Laut dem Verhalten in Abbildung 15 besteht dieser Energiezustand aus einer Reihe von Stufen, von denen jede eine Verzögerung oder Halbwertszeit für ihre Bildung und ihren Zerfall in das endgültige Fusionsprodukt aufweist. Diese Schlussfolgerung ergibt sich daraus, dass eine Reihe von Energieniveaus emittiert wird, von denen jedes eine geringere Wahrscheinlichkeit für seine Bildung hat, je höher die Energie ist, wie in den Abbildungen 13 und 16 dargestellt. Dies erfordert, dass jeder Energiezustand eine Verzögerung aufweist, bevor er „explodiert“, wobei während dieser Zeit zusätzliche Elektronen hinzugefügt werden können, um die Anordnung zu stabilisieren, bis der nächste instabile Zustand erreicht ist. Jeder dieser Schritte verringert die Wahrscheinlichkeit, eine Struktur mit einer größeren Anzahl von Elektronen zu erreichen. Warum und wie eine solche Abfolge von Strukturen entsteht, ist ein Problem, das theoretisch gelöst werden muss.

Der geschwindigkeitsbeschränkende Prozess, der die erzeugte Energiemenge kontrolliert, hängt von der Anzahl der aktiven Stellen und der Rate ab, mit der sich Elektronen und Wasserstoffkerne an jeder Stelle anlagern können. Die Temperatur, ein angelegter Elektronenstrom und ein angelegter Wasserstofffluss beeinflussen allesamt den Prozess des Zusammenschlusses. Sobald die aktive Struktur aufgebaut ist, verläuft der Fusionsprozess schneller als der Prozess des Aufbaus.

Im Zuge der Dissipation der freigesetzten Massenenergie müssen zur Impulserhaltung mindestens zwei Produkte des Fusionsmechanismus gleichzeitig zur Verfügung stehen. Die Elektronen, die diese Verringerung des Abstandes bewirken, wären in der Lage, mit den nuklearen Energiezuständen wechselzuwirken. Infolgedessen hätten einige dieser Elektronen während der Fusion Zugang zur freigesetzten Massenenergie und könnten diese Energie in Form von kinetischer Energie und Impuls abführen. Diese Elektronen müssen als enger Strahl emittiert werden, um den Impuls zu erhalten. Die in Abbildung 17 gezeigten engen Photonenstrahlen wären die Folge von Bremsstrahlung, wenn die Elektronen durch das umgebende Material hindurchgehen. Dieser Prozess wird auf Wikipedia unter Bremsstrahlung erklärt. Dieser Vorgang würde dazu führen, dass die Photonen eine bevorzugte Richtung aufweisen sowie eine Energie, die von der Energie der Elektronenstrahlen abhängt.

Weil viele Elektronen die D-Kerne umgeben und mit ihnen interagieren müssen, um die Barriere abzusenken und die Fusion zu ermöglichen, haben wir eine weitere Konsequenz zu berücksichtigen. Elektronen neigen aufgrund ihrer Abstoßungskräfte nicht dazu, sich in konzentrierten Ansammlungen zusammenzuschließen. Das bedeutet, dass eine neue Art von Elektronenwechselwirkung diese gegenseitige Abstoßung ausgleichen muss. Der Zusammenschluss muss auch eine quantisierte Eigenschaft aufweisen, um die in den Abbildungen 14 und 25 gezeigten Ergebnisse zu erklären. Somit wird eine neue Art von Elektronenstruktur offenbar, von der ich annehme, dass sie auch in normalen chemischen Systemen funktioniert, jedoch übersehen wurde, da die akzeptierte Erklärung des chemischen Verhaltens mit ausreichendem Erfolg ohne diese zusätzliche Komplexität auskam. Die beobachtete Produktion von Tritium im Erdmantel hat gezeigt, dass diese Kernreaktionen sogar unter normalen Umweltbedingungen stattfinden können. Eine Beschreibung basierend auf einer ähnlichen Ansammlung von Atomen und Elektronen wurde von Goncharov und Kirkinskii vorgeschlagen.

Da die Elektronen nicht durch den Mechanismus des Betazerfalls, d. h. durch den Zerfall eines Neutrons, emittiert werden, werden auch keine Neutrinos produziert. Dennoch würden beim normalen Betazerfall von ³H und ⁴H energiereiche Neutrinos entstehen, jedoch erst, nachdem die meiste Energie zuvor durch einen anderen Mechanismus dissipiert wurde, wodurch nur sehr wenig Energie für das Neutrino verbleibt, die es mit sich forttragen kann.

Der vorgeschlagene Kernprozess soll ein Wasserstoffisotop in ein anderes umwandeln. Die anfängliche Bildung von ⁴H aus der D-e-D-Fusion produziert ⁴H durch schnellen Betazerfall. Tritium, das aus der D-e-H-Fusion entsteht, produziert ³He durch langsamen Betazerfall. Einige wenige Neutronen entstehen, wenn das Tritium mit dem Deuterium fusioniert. Derselbe Mechanismus, einschließlich der Emission von Elektronen, gilt gleichermaßen für alle Wasserstoffisotope, wobei das nukleare Reaktionsprodukt nur davon beeinflusst wird, welches Isotop zur Fusion gebracht wird.

Diese Beschreibung ist in der Lage, die meisten der beobachteten Verhaltensweisen zu erklären, indem eine Reihe von Fragen mit konsistenter Logik beantwortet wird, ohne irgendwelche anerkannten Naturgesetze zu verletzen. Viele Vorhersagen werden getroffen, um die fünf Annahmen zu überprüfen. Darüber hinaus wird eine neuartige Wechselwirkung zwischen den Elektronen in einem Material identifiziert und einige Implikationen werden beschrieben, ohne sich mathematischer Annahmen zu bedienen.

Was hindert diese potenzielle Quelle sauberer Energie daran, in großem Maßstab genutzt zu werden? Schließlich ist dafür – im Gegensatz zur Heißen Fusion – keine gigantische und teure Struktur erforderlich. Stattdessen erfordert die Kalte Fusion lediglich spezielle Bedingungen, die sich in gewöhnlichen Materialien wie Palladium oder anderen Stoffen problemlos herstellen lassen. Die notwendigen Bedingungen könnten auch in großen Mengen mit reproduzierbarem Verhalten durch Nanobearbeitung geschaffen werden. Die Erkenntnis darüber, wie die Kalte Fusion nutzbar gemacht werden kann, hat sich nur deshalb verzögert, weil der bisherige Aufwand, das notwendige Verständnis hierfür zu erlangen, im Vergleich zur tatsächlichen Schwierigkeit des Problems zu gering war. Nichtsdestotrotz wird dieses Problem allmählich gelöst. Es bleibt zu hoffen, dass die vorliegende Abhandlung zu einer Beschleunigung dieser Bemühungen beitragen wird.

Danksagung

Ohne die finanzielle Unterstützung und die Ermutigung durch Brian Scanlan wäre dieser Artikel nicht möglich gewesen. Auch Bruce Steinetz und Larry Forsley leisteten wichtige Unterstützung und ermöglichten die finanzielle Förderung durch die NASA. Meine Frau Carol hat meine Bemühungen durch ihre Geduld und ihre Liebe unterstützt. George Hulse und David Nagel bin ich dankbar, dass sie mich ermutigt haben, die Beschreibung zu präzisieren. Dank der Arbeit von Jed Rothwell sind viele der zitierten Arbeiten auf LENR-CANR.ORG zu finden.

Anhang I

Zusammenfassung der Implikationen.

1. ⁴He wird nicht direkt durch den Fusionsprozess erzeugt.
2. ⁴He wird nicht mit Energie emittiert.
3. ⁴He resultiert aus dem schnellen Betazerfall von ⁴H.
4. ⁴H wird erzeugt und mit Energie emittiert, wenn D fusioniert
5. Ein komplexer Prozess, der die Anordnung von Elektronen umfasst, findet in einem Material an einzigartigen Stellen statt.
6. Ein komplexer Prozess, der einzigartig verwandte Energiezustände verursacht, führt zum Ereignis der Kalten Fusion.
7. Tritium wird gebildet, wenn D+H fusionieren.
8. Bei einer H+H-Fusion entsteht weniger Energie als bei einer D+D-Fusion.
9. Die emittierte Energie des ⁴H ist ausreichend, um Transmutationen zu bewirken und Reaktionsprodukte der Heißen Fusion zu erzeugen.
10. Die Fraktofusion kann eine Folge einer kurzen kalten Fusionsreaktion sein.
11. Es werden sehr energiereiche Elektronenstrahlen emittiert, die Photonenstrahlen hervorrufen.
12. Der Prozess erzeugt Magnetfelder und würde von einem angelegten Magnetfeld beeinflusst werden.
13. Der Prozess erfordert Spalten mit einer kritischen Größe.
14. Die Verwendung von normalem H führt zu einem größeren He/Energie-Verhältnis im Vergleich zur Verwendung von reinem D.
15. Ein praktisches Generatordesign erfordert die Fähigkeit, die Temperatur zu erhöhen, einen Strom durch das Material zu leiten, ein Magnetfeld anzulegen und die NAE durch Nanobearbeitung zu bilden.