Zero-Point Energy: Capturing Evanescence

Nullpunktsenergie: Das Einfangen der Flüchtigkeit

Journal of Scientific Exploration
Garret Moddel, Department of Electrical, Computer, and Energy Engineering
22. Oktober 2022
Zero-Point Energy: Capturing Evanescence

Schwerpunkte

Eine Kombination der Konzepte zum Quantenvakuum mit denen zu nanoelektronischen Bauelementen führt zu einem neuartigen energieerzeugenden Bauelement, welches offensichtlich Energie aus dem Quantenvakuum gewinnt.

Zusammenfassung

Die Ergebnisse aus Tausenden von Versuchen und aus Dutzenden von Variationen, aus Tests bezüglich Messartefakten sowie aus Replikationen haben ergeben, dass Vorrichtungen mit einem Metall/Isolator/Metall-Casimir-Hohlraum offenbar in der Lage sind, elektrische Energie zu generieren, indem sie die Nullpunktsenergie (NPE) ihrer Umgebung anzapfen. Schon eine einfache Kalkulation ergibt, dass die potenziell zur Verfügung stehende Energie des NPE-Quantenvakuums immense 5 Gigawatt pro Quadratmeter beträgt. Die Bauelemente zapfen davon nur einen winzigen Bruchteil an, erreichen aber dennoch eine praktische Leistungsdichte von 70 Watt pro Quadratmeter. Die Bauelemente wurden entwickelt, um die offensichtlichen Hindernisse, die der Gewinnung der NPE entgegenstehen, zu umgehen, die darin bestehen, dass es sich bei der NPE um den universellen Grundzustand handelt und dass die Fluktuationen der NPE extrem kurzlebig und quasi nur virtuell existieren. Sollte sich letztendlich herausstellen, dass es sich bei der Quelle um die NPE handelt, stellt sich die Frage, welches Funktionsprinzip hinter der Energiegewinnung steht und wie die Ergebnisse mit den bekannten physikalischen Gesetzen in Einklang gebracht werden können. Als gedankliches Funktionsprinzip lässt sich eine direkte Analogie zum dem optischen Phänomen der frustrierten Totalreflexion verstehen. Legt man die herkömmliche Quanteninterpretation der NPE zugrunde, so verstößt das Anzapfen der NPE zwar nicht gegen den Zweiten Hauptsatz der Thermodynamik, aber die Frage nach der Quelle der NPE bleibt weiterhin ungeklärt.

Einführung

Im Laufe der Menschheitsgeschichte hat sich das Konzept des Ressourcenverbrauchs zur Gewinnung von Energie mittels des Abbaus von kohlenstoffhaltigen Brennstoffen, der Nuklearreaktion von Kernbrennstoffen, des Einfangens von Sonnenlicht und dergleichen zur Energiegewinnung durchgesetzt. Aus dieser Perspektive erscheint die Gewinnung von Nullpunktsenergie (NPE), in der immer noch ein rätselhafter Schatz an allgegenwärtiger Energie schlummert, wie ein Verstoß gegen alle Grundlagen unserer Welt, wie wir sie bisher verstanden haben. Können wir diese Energie anzapfen, oder würde dies gegen grundlegende Prinzipien verstoßen? Es sieht ganz danach aus, dass unser Labor tatsächlich einen Weg gefunden hat, wie sich die NPE anzapfen lässt (Moddel u. a. 2021a; Moddel, 2021c). In diesem Artikel gehe ich darauf ein, wie wir dies erreicht haben, und beschreibe die zugrunde liegenden Fragen. Zunächst geht es um die Grundlagen der NPE, einschließlich der Frage, wie viel Energie aus dem Quantenvakuum der NPE gewonnen werden kann. Es folgen die Technologie, die wir entwickelt haben, um diese zu nutzen, und schließlich die Ergebnisse. Dann untersuche ich die Hindernisse, die der Nutzung von NPE-Fluktuationen noch im Wege stehen, einschließlich einer Möglichkeit, die Energiegewinnung über sogenannte virtuelle Teilchen zu verstehen. Der Artikel befasst sich ferner mit der Frage, ob die Gewinnung von NPE gegen den Zweiten Hauptsatz der Thermodynamik verstoßen würde und woher die Energie letztlich kommen könnte. Im Anhang finden sich die Gleichungen und Berechnungen zur verfügbaren Energie sowie eine Beschreibung der Sicherheitsüberprüfungen, die wir durchgeführt haben, um zu untersuchen, ob sich die Ergebnisse auf nicht berücksichtigte Artefakte zurückführen lassen. Derzeit befinden wir uns noch mitten in der Forschung, und dieser Artikel gibt unseren derzeitigen Kenntnisstand wieder, der sich mit der Zeit sicher noch weiterentwickeln wird.

Hintergrundinformationen zur Nullpunktsenergie

Bei der NPE handelt es sich um die Energie des Grundzustandes von quantenmechanischen Systemen sowohl im leeren Raum als auch in der Materie. Im leeren Raum führt sie zu Fluktuationen des elektromagnetischen Feldes (Milonni, 2013). In Molekülen und Festkörpern regt sie Schwingungen (quantisiert als Phononen) an (Yang & Kawazoe, 2012). Kommen dann auch noch leitende Ladungsträger (wie etwa Elektronen) hinzu, führt dies zu plasmonischen Fluktuationen (kollektive Ladungsschwingungen) (Rivera et al., 2019).

Im Jahr 1900 entwickelte Max Planck seine revolutionäre Theorie der Schwarzkörperstrahlung, welche den Raum ausfüllt. In Abbildung 1 ist diese thermische Schwarzkörperstrahlung als abwärts verlaufende Kurve für die Raumtemperatur (300 K) dargestellt. Sie erreicht ihren Höhepunkt bei einer Photonenenergie von etwa 0,1 eV, was einer Wellenlänge im Infrarotbereich von 12 μm entspricht, und fällt dann ab, bevor sie das sichtbare Spektrum erreicht.

Abbildung 1. Die Energiedichte der elektromagnetischen Hintergrundfelder bei Raumtemperatur (T = 300 K) als Funktion der Photonenenergie (Darstellung von Matt McConnell).

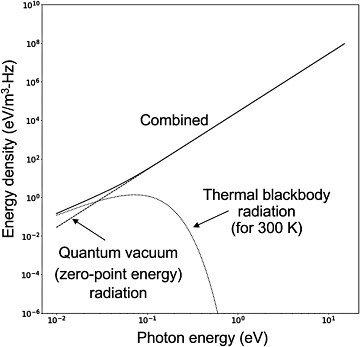
Eleven years after presenting his first theory Planck presented his second theory, which contained an additional, temperature-independent term. The full expression for the energy density of both the thermal blackbody, at temperature T, and ZPE components is Elf Jahre nach seiner ersten Theorie präsentierte Planck seine zweite Theorie, die einen zusätzlichen, temperaturunabhängigen Term enthielt. Der vollständige Ausdruck für die Energiedichte sowohl des thermischen Schwarzkörpers mit der Temperatur T als auch der Komponenten der NPE lautet

[math]\rho(hf) = \frac{8 \pi f^2}{c^3} \left( \frac{hf}{exp (hv / kT) - 1} + \frac{hf}{2} \right)[/math],

(1)

wobei h die Plancksche Konstante, f die Frequenz der Strahlung und c die Lichtgeschwindigkeit darstellen (Milonni, 2013). Die zuletzt aufgeführte Komponente, die als zweiter Term auf der rechten Seite der Gleichung erscheint, bezeichnete Planck als Restenergie (Kragh 2012). Zwei Jahre später bezeichneten Albert Einstein und Otto Stern sie als Nullpunktsenergie (NPE), da sie auch noch bei einer Temperatur von null vorhanden ist. 1916 stellte Nernst fest, dass die NPE nicht nur den Raum (den er Äther nannte), sondern auch materielle Objekte erfüllt. Damals wurden sowohl Plancks zweite Theorie als auch der Begriff der NPE von der Physikergemeinde abgelehnt und erst ab 1926 in zunehmendem Maße akzeptiert, als die Unschärferelation innerhalb der sich damals entwickelnden Quantenmechanik dies erforderlich machte. Abbildung 1 zeigt die Energiedichte für die NPE als gerade Linie. Bei Photonenenergien, die oberhalb jener des mittleren Infrarotlichtes liegen, dominiert im Energiespektrum der NPE-Anteil.

Normalerweise ist die Energiedichte der NPE gegeben. Diese hat allerdings für die Gewinnung der Energie keine unmittelbare Relevanz. Für die Gewinnung von Energie ist der Energiefluss, d. h. die Leistung und die Stromstärke, von Bedeutung. In Anhang I leite ich den mathematischen Ausdruck für diese Größen ab und ermittle den kumulativen Wert bis zu einer bestimmten (Grenz-)Photonenenergie. Die kumulative Stromdichte wächst mit der dritten Potenz der Grenzphotonenenergie (hf) und die Leistungsdichte mit der vierten Potenz der Grenzphotonenenergie. Die Strahlung, die eine bestimmte Fläche durchdringt, lässt sich in Form des Photonenstroms ausdrücken, der als der elektrische Strom definiert ist, welcher erzeugt werden würde, wenn jedes einfallende Photon den Strom eines Elektrons erzeugen würde. Der kumulative Photonenstrom der NPE wird in Abbildung 2 dargestellt.

Abbildung 2. Kumulativer Photonenstrom bei Raumtemperatur bis zu einer Grenzphotonenenergie aus der elektromagnetischen Hintergrundstrahlung, wobei es sich bei den beiden Größen um den thermischen Schwarzkörper und das Quantenvakuum (Nullpunktsenergie) handelt. Der Photonenstrom ist definiert als der elektrische Strom, der für jedes einfallende Photon erzeugt würde, welches den Strom aus einem einzelnen Elektron erzeugt. Die Herleitung des Ausdrucks für diese Ströme findet sich in Anhang I.

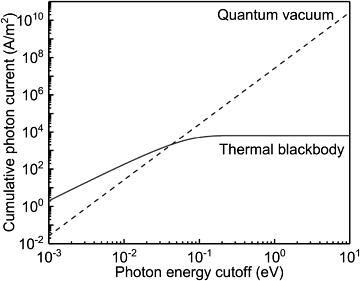
Die kumulativen Photonenströme aus dem Spektrum der NPE sind gigantisch. Zum Beispiel beträgt der erzeugte Strom bei einer Grenzphotonenenergie von 4 eV, was einer Wellenlänge von 0,3 μm entspricht, 1,7 GA m-2, d. h. mehr als eine Milliarde Ampere pro Quadratmeter. Zum Vergleich: Eine Solarzelle erzeugt etwa 350 A m-2.

Die aus dem Quantenvakuum verfügbare Leistung für dieselbe Grenzphotonenenergie von 4 eV beträgt nach den Berechnungen im Anhang I 5,0 GW m-2. Zum Vergleich: Ein Kohlekraftwerk erzeugt insgesamt etwa 5 GW, also die gleiche Menge an NPE, die einen Quadratmeter durchdringt. Wie weiter unten beschrieben, beträgt die von uns bisher ermittelte Leistungsdichte weitaus weniger als die verfügbare Leistung, reicht aber völlig aus, um praktikable Leistungswerte zu erzielen.

Gerätebeschreibung und Ergebnisse

Der Geräteaufbau

Abbildung 3(a) zeigt den Querschnitt eines der Geräte, die in unserem Labor gefertigt werden.

Abbildung 3: (a) Querschnitt durch das Bauelement, der eine Metall/Isolator/Metall-Struktur (MIM) zeigt, welche an einen optischen Hohlraum angrenzt. Der positive Strom fließt in Richtung des Pfeiles. (b) Eine rasterelektronenmikroskopische Aufnahme der Draufsicht eines fertigen MIM-Bauelementes. Beide Bilder stammen aus der Veröffentlichung von Moddel (2021a).

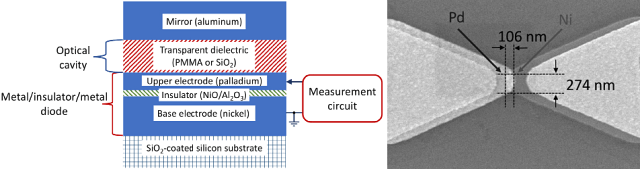
Das Bauelement besteht aus einem optischen Hohlraum, der auf einer Metall/Isolator/Metall (MIM)-Diode aufgebracht ist. Der optische Hohlraum, auch Casimir-Hohlraum genannt, besteht, wie später in diesem Artikel noch erläutert werden wird, aus zwei reflektierenden Schichten, welche ein transparentes dielektrisches Medium umgeben – entweder ein Polymer, genauer gesagt Polymethylmethacrylat (PMMA), oder das Oxid SiO2. Die Stärke des Hohlraumes beträgt zwischen 33 nm und 1100 nm. Die MIM-Diode besteht aus einer halbtransparenten Palladiumschicht mit einer Stärke von 8,3 nm und einer dickeren Nickelschicht, die einen sehr dünnen Isolator mit einer Stärke von 2 nm umgibt. Der Isolator ist so dünn, dass ihn Ladungsträger durchtunneln können.

Die Bauelemente werden mit den in Moddel u.a. (2021a) beschriebenen Mikrofertigungstechniken hergestellt. Es wurden zwar Bauelemente mit einer breiten Palette an Flächen hergestellt, doch die höchste Leistungsdichte wurde bisher mit jenen erreicht, die im Submikrometerbereich liegen. Abbildung 3(b) zeigt eine rasterelektronenmikroskopische Aufnahme eines der Bauelemente. Der aktive Bereich, der aus der Überlappung von Palladium- und Nickelbereichen mit einem dünnen Isolator zwischen beiden besteht, weist eine Fläche von 0,02 μm2 auf. Über der MIM-Struktur ist ein optischer Casimir-Hohlraum ausgebildet worden.

Die Ergebnisse

Das Vorhandensein eines angrenzenden optischen Hohlraumes hat dazu geführt, dass die Strom-Spannungs-Kennlinie I(U) der MIM-Diode radikal verändert wird. Ihr Widerstand wird hierdurch erheblich reduziert (Moddel, 2021b). Aber von noch entscheidender Bedeutung ist, dass es hierdurch zu einer Erzeugung von elektrischer Energie kommt. In Abbildung 4(a) ist die I(U)-Kurve für ein Bauelement mit einem 33 nm dicken transparenten Dielektrikum dargestellt.

Abbildung 4. (a) Strom als Funktion der Spannung für ein Bauelement mit einem 33 nm großen, mit PMMA gefüllten Hohlraum. Die Kurve verläuft durch den zweiten Quadranten des Diagrammes, der für die Erzeugung von elektrischer Energie steht. Die Leistungsdichte beträgt 70 W/m2.

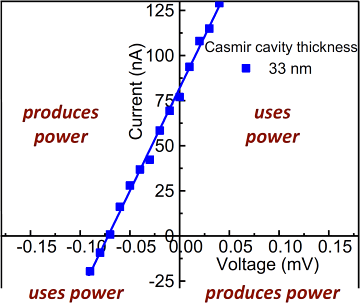
Verläuft eine I(U)-Kurve nicht durch den Ursprung, kommt es zum Verbrauch oder zur Erzeugung von elektrischer Energie (I × U), wobei der zweite und der vierte Quadrant der I(U)-Kurve jeweils für die Erzeugung von elektrischer Energie stehen.

Bemerkenswert daran ist die Tatsache, dass das Bauelement einen elektrischen Strom erzeugt, ohne dass es hierfür einen offensichtlichen Energiezufluss gibt. Die Kennzahlen für die Fläche und die I(U)-Kennlinie des gezeigten Bauelementes entsprechen einer Energieerzeugung von 70 W/m2. Das entspricht etwa einem Drittel der von Solarzellen erzeugten Leistung pro Flächeneinheit. Da dieses Bauelement noch keine Optimierung erfahren hat und sich prinzipiell stapeln lässt, sind für die Zukunft sehr beachtliche und praktikable Leistungswerte zu erwarten – vorausgesetzt, dass sich dieses Konzept in der Weise skalieren lässt, wie es offenbar der Fall ist.

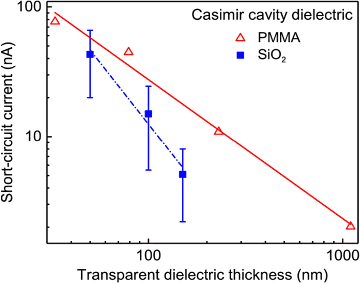
Wie später in diesem Artikel noch erläutert wird, zeichnet sich die NPE dadurch aus, dass die Energiedichte mit abnehmender Stärke des optischen Hohlraumes immer weiter sinkt. Die Werte in Abbildung 4(b) weisen genau einen solchen Trend auf, wobei die Leistung von Bauelementen für schmalere Hohlräume, welche mit PMMA oder mit SiO2 gefüllt sind, zunimmt.

Abbildung 4: (b) Kurzschlussstrom als Funktion der Kavitätsstärke für PMMA- und SiO2-gefüllte Kavitäten (aus Moddel, 2021a). Die Leistung nimmt mit zunehmender Stärke des Hohlraumes ab, ein Zeichen für NPE.

Die Überprüfung auf Artefakte

Die hier dargestellten Trends wurden in vielen Tausenden von Bauelementen reproduziert, welche wiederum in Dutzenden von Chargen gefertigt wurden, wenn auch mit erheblichen Variationen von Bauelement zu Bauelement, was auf die unzulänglich kontrollierten Herstellungsparameter unseres derzeitigen Fertigungsprozesses zurückzuführen ist. Um zu überprüfen, ob die Bauelemente tatsächlich Strom erzeugen, wurden von uns neun mögliche Artefakte eingehend untersucht (Moddel 2021a). Die wichtigsten Ergebnisse finden sich zusammengefasst in Anhang II. Nach unserem Kenntnisstand kann kein mögliches Artefakt für die beobachteten Ergebnisse verantwortlich gemacht werden.

Die Hindernisse auf dem Weg zur Gewinnung von Nullpunktsenergie

Der allgemeine Grundzustand

Bei der NPE handelt es sich um den allgemeinen Grundzustand, und daraus ergibt sich, dass sich ohne einen Gradienten (Neigung) oder eine Stufe in der Dichte der NPE keine Strömung ausbilden kann. Eine Veränderung dieses Grundzustandes lässt sich jedoch herbeiführen, denn diese ist abhängig von der Geometrie. Im Jahr 1948 schlug Hendrik Casimir vor, dass die Dichte der NPE zwischen zwei eng benachbarten Spiegeln geringer ist als außerhalb von ihnen (Casimir, 1948). So sind in diesem Casimir-Hohlraum nur solche elektromagnetischen Nullpunktsmoden möglich, deren Wellenlänge das Doppelte des Abstandes des optischen Hohlraumes geteilt durch eine Ganzzahl beträgt – und alle Wellenlängen, die größer als das Doppelte des Abstandes sind, sind blockiert. Die Verringerung der Modendichte ist in Abbildung 5 dargestellt.

Abbildung 5. Darstellung der optischen Moden in einem Casimir-Hohlraum, in dem nur bestimmte Wellenlängen möglich sind und langwellige elektromagnetische Nullpunktsmoden blockiert sind (Abbildung aus Kingsbury [2009]).

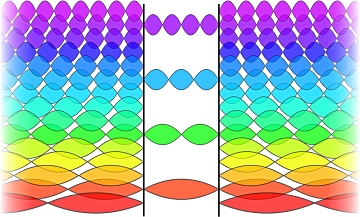
Wie noch zu zeigen sein wird, nutzen unsere Bauelemente einen angrenzenden optischen Hohlraum, um in der Dichte der NPE eine Stufe auszubilden.

Kurzlebige Fluktuationen

Die Heisenbergsche Unschärferelation beschreibt die Begrenztheit in der Genauigkeit, mit der die Werte bestimmter komplementärer Paare von physikalischen Größen gemessen werden können. Ein solches Paar ist die Energie und die Zeit. Je geringer die Ungenauigkeit in der Energie (ΔE) eines Teilchens ist, desto größer muss die Ungenauigkeit in der Zeit (Δt) sein, in der dieses beobachtet werden kann. Für ein Vakuum bedeutet dies, dass die Fluktuationen der NPE von großer Energie nur für kurze Zeit bestehen können. Zum Beispiel bestehen Fluktuationen mit einer Photonenenergie von 2 eV (entspricht rotem Licht) nur für die Dauer von 0,16 fs (eine Femtosekunde beträgt 0,000 000 000 000 001 Sekunden). Es wurde die Theorie entwickelt, nach der eine Energie ΔE für eine Dauer Δt aus dem Vakuum geliehen werden kann, solange diese wieder zurückgegeben wird (Ford, 1991; Davies & Ottewill, 2002; Huang & Ford, 2015). Daher habe ich mir die Frage gestellt, was geschehen würde, wenn die Energie der Fluktuation auf extrem schnelle Weise eingefangen werden könnte, so dass sie nicht wieder zurückgegeben werden kann. Wie im Abschnitt zum Gerätekonzept erläutert, nutzen unsere Bauelemente den femtosekundenschnellen Einfang transitorischer energieaufgeladener Teilchen.

Virtuelle Teilchen

Trifft eine ausreichend große Menge an elektromagnetischer Strahlung auf eine Metalloberfläche, werden durch diese Elektronen emittiert, wie in Abbildung 6 dargestellt. Dieser photoelektrische Effekt wurde 1887 von Heinrich Hertz beobachtet und 1905 von Einstein mit Bezug auf die Photonenenergie erklärt.

Abbildung 6. Der photoelektrische Effekt, bei dem die auf eine Metalloberfläche auftreffende elektromagnetische Strahlung die Emission von Elektronen bewirkt. (Bild aus Wikimedia Commons, https://commons.wikimedia.org/wiki/File:Photoelectric_effect.svg)

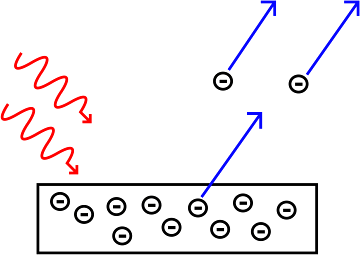
Angesichts der allgegenwärtigen elektromagnetischen Nullpunktshintergrundfelder, wie sie in Abbildung 1 dargestellt sind, stellt sich die Frage, warum sich die Emission von Elektronen infolge dieser Felder nicht bei sämtlichen Metalloberflächen beobachten lässt. Die Antwort auf diese Frage liegt in der Kurzlebigkeit der im vorangegangenen Abschnitt beschriebenen Fluktuationen. Für das oben beschriebene Beispiel einer 2 eV-Strahlung (rotes Licht) beläuft sich dieser Wert auf lediglich 0,16 fs. Eine einfache Berechnung zeigt, dass ein Elektron in dieser Zeit eine Strecke von gerade einmal 1 Å (0,1 nm) zurücklegen würde, was in etwa der Entfernung zwischen zwei Atomen entspricht, bevor die geliehene Fluktuationsenergie zurückgegeben sein würde.

Eine andere Vorstellung von kurzlebigen Fluktuationen beruht auf dem Konzept der virtuellen Teilchen. Obwohl eine Unterscheidung zwischen realen und virtuellen Teilchen umstritten ist (Jaeger, 2019), werden elektromagnetische Wellen im Quantenvakuum der NPE im Allgemeinen als virtuell betrachtet. Bei virtuellen Wellen und Teilchen handelt es sich demnach um flüchtige Quantenfluktuationen, deren Existenz durch die Unschärferelation zeitlich begrenzt ist, und über die die Wechselwirkungen zwischen den anderen Teilchen vermittelt werden. Da sie nur über ihre Auswirkungen auf andere Teilchen beobachtet werden können, lässt sich ein „bloßes“ virtuelles Teilchen nicht einfangen. Sie lassen sich jedoch in reale Teilchen umwandeln. Im Zusammenhang mit dem dynamischen Casimir-Effekt hat sich gezeigt, dass die effektive Bewegung der Spiegel eines Casimir-Hohlraumes, die mit hoher Geschwindigkeit erfolgt, dazu führt, dass virtuelle Fluktuationen in reale Photonen umgewandelt werden (Wilson et al., 2011). Lassen sich also durch das ultraschnelle Einfangen auch virtuelle Teilchen in reale umwandeln? Ausgehend von einem Vergleich mit evaneszenten optischen Moden behaupte ich, dass die Antwort „ja“ lauten könnte.

Bei evaneszenten Wellen handelt es sich um oszillierende elektromagnetische Wellen, die sich nicht ausbreiten, sondern einfach nur an einem Ort verbleiben. Solche evaneszenten Wellen gleichen virtuellen Photonen (Stahlhofen, 2006). Eine solche evaneszente Welle entsteht an einer Grenzfläche, an der es zu einer Totalreflexion kommt. Bei der Totalreflexion handelt es sich um ein optisches Phänomen, welches in einem Prisma auftritt, wenn das Licht in einem Winkel einfällt, der größer ist als der kritische Winkel, so wie in Abbildung 7(a) dargestellt.

Abbildung 7. Umwandlung von evaneszenten Wellen in sich ausbreitende Wellen. (a) Interne Totalreflexion in einem Prisma, wobei sich die evaneszente Welle über das Prisma hinaus ausbreitet. (b) Ein zweites Prisma, das mehrere Wellenlängen vom ersten Prisma entfernt ist, beeinflusst diese evaneszente Welle in keiner Weise. (c) Ein zweites Prisma, das nur den Bruchteil einer Wellenlänge vom ersten Prisma entfernt ist, verhindert die Totalreflexion und führt zu einer sich ausbreitenden Welle. Eine Bemerkung am Rande: Der Abstand der evaneszenten Kopplung wird durch dieselbe ΔEΔt-Unschärferelation begrenzt, welche auch die Nullpunktsfluktuationen kontrolliert (Moddel, unveröffentlicht).

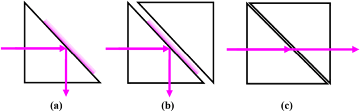
Die evaneszente Welle reicht über das Prisma hinaus, fällt aber innerhalb eines Bruchteils der Wellenlänge exponentiell ab. Wird ein zweites Prisma in einem Abstand von mehr als einer Wellenlänge vom ersten platziert, so wie in Abbildung 7(b) dargestellt, wird die evaneszente Welle hiervon nicht beeinflusst. Befindet sich das zweite Prisma jedoch nur einen winzigen Bruchteil einer Wellenlänge vom ersten entfernt, kommt es zu einer evaneszenten Kopplung – die zuvor stationäre Welle verwandelt sich in eine sich ausbreitende Welle, so wie in Abbildung 7(c) dargestellt. Auf diese Weise wird die Totalreflexion verhindert (Hecht, 2017). Durch die Nähe zu einem zweiten Prisma verwandelt die evaneszente Welle sich also in eine sich ausbreitende Welle – ein sichtbares Beispiel für das Quantentunneln durch den engen Spalt.

Der gleiche Prozess ereignet sich in unseren Bauelementen, in denen eine abklingende Welle sich an einer Barriere zu einer sich ausbreitenden Welle verwandelt, wenn der Barrierebereich nur dünn genug ist. Dies ist in Abbildung 8 dargestellt, wo die einfallende Welle aus den Elektronen in einer Metallschicht (wie der oberen Elektrode in unserem Bauelement) besteht.

Abbildung 8. Die evaneszente Kopplung in einem Metall/Isolator/Metall-Bauelement. Der Isolator bildet eine Barriere, die von der Elektronenwelle quantenmechanisch durchtunnelt wird, was einer evaneszenten Kopplung gleichkommt. Das Quantentunneln unterliegt der gleichen ΔEΔt-Unschärferelation, durch die auch die Nullpunktsfluktuationen beschränkt werden (Fertig, 1990). (Abbildung reproduziert aus Bhansali et al., 2010).

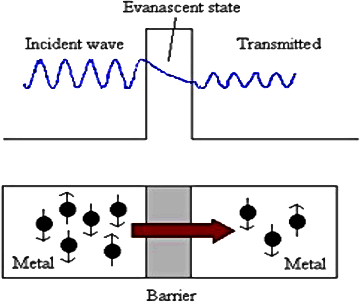
Die Barriere stellt einen Isolator dar. Ist diese Isolatorschicht ausreichend dünn, dann tunnelt ein Teil der Elektronenwelle hindurch und wird auf die zweite Metallschicht (in unserem Bauelement die Basiselektrode) übertragen. Die energiereichen Elektronen werden dann in dieser zweiten Metallschicht sofort eingefangen. Wie im nächsten Abschnitt beschrieben, bildet dieser Elektronentransport den zweiten Schritt innerhalb einer Kette von virtuellen Teilchen.

Das Konzept des Bauelementes

Das Konzept für das Bauelement zur Gewinnung von NPE wurde vor fünf Jahren entwickelt und vor drei Jahren zur vorläufigen Patentanmeldung eingereicht – und vor Kurzem wurde das Patent erteilt (Moddel, 2021c). Nachfolgende experimentelle Ergebnisse haben gezeigt, dass die effektive Struktur und die Ausgangscharakteristik des Bauelementes, die in den Abbildungen 3 und 4 dargestellt sind, exakt dem entsprechen, was prognostiziert wurde. Das Funktionieren des Bauelementes scheint, wie weiter unten beschrieben, das Ergebnis einer Asymmetrie zu sein, welche durch das Vorhandensein eines angrenzenden Casimir-Hohlraumes hervorgerufen wird. Derzeit handelt es sich bei diesem Funktionsmodell noch um eine spekulative Variante, und es ist durchaus möglich, dass der Aufbau des Gerätes die Energiegewinnung rein zufällig mittels eines ganz anderen Mechanismus ermöglicht hat. Im Folgenden beschreibe ich das offensichtliche Funktionsprinzip.

Das Bauelement für die Gewinnung von NPE basiert auf MIM-Dioden – Bauelementen, welche durch unser Labor bereits seit mehr als zwei Jahrzehnten entwickelt und gefertigt werden, um eine extrem schnelle Gleichrichtung zu erzielen (Grover & Moddel, 2012). Diese Bauelemente funktionieren mittels einer ultradünnen Barriere, die den Ladungsträgern, also den Elektronen oder den Elektronenlöchern, das Tunneln ermöglicht (siehe Abbildung 8). (Obwohl sich der Begriff „Diode“ in der Regel auf Bauelemente bezieht, die den Strom bevorzugt in eine Richtung fließen lassen, weisen die MIM-Dioden bezüglich des Stromflusses nicht notwendigerweise eine Asymmetrie auf.) Das Durchtunneln bzw. die Anregung durch den 1 bis 3 nm dicken Isolator erfolgt innerhalb von etwa 1 fs. Die Bauelemente zur Gewinnung der NPE weisen MIM-Dioden auf, die über eine ausreichend dicke Basisschicht (> 35 nm) verfügen, um undurchsichtig zu sein, sowie über eine dünnere (~10 nm) halbtransparente obere Elektrode.

Der photoelektrische Effekt, wie in Abbildung 6 dargestellt, führt an der offenen Oberfläche zur Emission von Elektronen. Ist die Metallschicht ausreichend dünn, so erzeugen die angeregten Elektronen an der inneren Oberfläche auch noch eine interne Photoemission (auch Photoinjektion genannt). Abbildung 9(a) zeigt eine MIM-Diode mit einer halbtransparenten oberen Elektrode.

Abbildung 9. Querschnitte der Bauelemente zur Veranschaulichung des Funktionsprinzips. (a) MIM-Diode mit einer dünnen oberen Elektrode, welche die Photoinjektion von Ladungen aus elektromagnetischen Nullpunktsfluktuationen des freien Raumes ermöglicht. Der Abwärtsfluss der photoinjizierten Ladung sowie der intern angeregten Ladung wird durch den Aufwärtsfluss der intern angeregten Ladung ausgeglichen. (b) MIM-Diode mit einem angrenzenden Casimir-Hohlraum über der oberen Elektrode, welcher zur Unterdrückung der Photoinjektion führt und den Abwärtsfluss der Ladung reduziert.

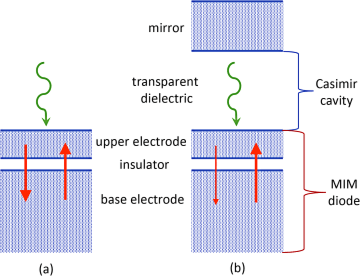
An der oberen Oberfläche regt die einfallende Nullpunktsstrahlung heiße Ladungsträger an, welche zum Abwärtsfluss von Ladungen beitragen. Darüber hinaus regen auch interne NPE-Fluktuationen in der oberen Elektrode Ladungen an, die ebenfalls zu diesem Abwärtsfluss beitragen. Die Kombination aus Photoinjektion und intern angeregten Ladungen führt zu dem durch einen Pfeil auf der linken Seite dargestellten Abwärtsfluss. Der effektiv erzeugte Strom unterliegt denselben Beschränkungen, die jeden durch die NPE angeregten Strom, wie er durch die in Abbildung 6 gezeigte photoelektrische Konfiguration hervorgerufen wird, blockieren. Ich bezeichne dies vereinfacht als virtuellen Strom.

In ähnlicher Weise werden durch interne Fluktuationen der NPE in der Basiselektrode Ladungen angeregt, die zu einem Aufwärtsstrom führen. Es existiert jedoch kein Photoinjektionsstrom, der zu diesem Aufwärtsstrom beitragen könnte, da die Basiselektrode zu dick ist, als dass die an der unteren Oberfläche erzeugten photoangeregten Ladungen die Elektrode bis zum Isolator durchqueren könnten, bevor sie gestreut werden. Da die Basiselektrode dicker ist als die obere Elektrode, werden durch sie mehr interne Ladungen erzeugt, wodurch der gesamte aufwärts gerichtete Ladungsfluss gleich dem abwärts gerichteten ist.

Ziehen wir nun eine identische MIM-Diode in Betracht, die über der oberen Elektrode zusätzlich einen Casimir-Hohlraum besitzt, so wie in Abbildung 9(b) dargestellt. Wie bereits in Abbildung 5 gezeigt, weist die elektromagnetische Nullpunktsmodendichte in einem Casimir-Hohlraum einen niedrigeren Wert auf als die Modendichte im freien Raum. Dadurch ist der Photoinjektionsstrom partiell reduziert und der abwärts gerichtete Ladungsfluss verringert. Da der zusätzliche Casimir-Hohlraum auf den Aufwärtsstrom keinen negativen Einfluss hat, ergibt sich nun ein Nettoladungsfluss in Aufwärtsrichtung. Bezüglich des beobachteten Stroms handelt es sich um eine vereinfachte konzeptionelle Erklärung. Die tatsächlichen Mechanismen sind jedoch wesentlich komplexer und beinhalten sowohl die Emission elektromagnetischer Moden in den Hohlraum hinein als auch die Absorption aus dem Hohlraum heraus. Diese unterliegen den Einschränkungen der Unschärferelation, da die Nullpunktsanregungen transienter Natur sind und sowohl Elektronen als auch Elektronenlöcher zu dem Strom beitragen können.

Zu der Ereigniskette, die das Einfangen von NPE möglich macht, kann ich nur spekulieren. Virtuelle Photonen treffen auf die obere Elektrode und erzeugen einen virtuellen Strom von Ladungsträgern, welcher dann die dünne Metallschicht und den Isolator durchquert und schließlich in der Basiselektrode eingefangen wird. Genauso wie virtuelle Photonen, die eine evaneszente Welle bilden, in reale, sich ausbreitende Photonen umgewandelt werden, sofern eine evaneszente Kopplung vorhanden ist, werden auch die virtuellen Photonen und der anschließende virtuelle Ladungsstrom in einen realen Ladungsstrom umgewandelt, der den Isolator durchtunnelt und in der Basiselektrode unserer Bauelemente eingefangen wird. Anstatt sich auf den Begriff der virtuellen Teilchen zu beziehen, begrenzt die Unschärferelation ΔEΔt die Zeit, die für diesen Prozess zur Verfügung steht. Gelingt es, den Transit und das Einfangen innerhalb von etwa 1 fs zu absolvieren, lässt sich die Energie einfangen – anderenfalls wird die Energie wieder zurückgegeben. Selbst wenn der Prozess nicht innerhalb der im Abschnitt über kurzlebige Fluktuationen beschriebenen 0,16 fs abgeschlossen werden kann, lässt sich ein gewisser Teil des verfügbaren Stroms einfangen, auch durch Anregungen mit niedrigerer Energie und daher von längerer Lebensdauer. Das Vorhandensein des angrenzenden Casimir-Hohlraumes stört das Gleichgewicht des virtuellen Ladungsflusses, das mit diesem bestehen würde, so dass der Nettoladungsfluss nach oben gerichtet ist.

Dieses Funktionsmodell ist bestenfalls hypothetisch zu nennen und bei weitem nicht stringent. Hingegen wurde ein strenges Quantenmodell (Ford, 2022) vorgeschlagen, um den Anstieg der Leitfähigkeit zu erklären, der sich infolge eines angrenzenden Casimir-Hohlraumes (Moddel, 2021b) einstellt – das die beobachtete Energieerzeugung jedoch nicht zu erklären vermag.

Die Hauptsätze der Thermodynamik

Der Zweite Hauptsatz der Thermodynamik beschreibt die Grenzen jener Wärmemenge, die sich in Arbeit umwandeln lässt, sowie die Unmöglichkeit der Umwandlung von Wärme in Arbeit, wenn diese die gleiche Temperatur besitzt wie ihre Umgebung. Vom Zweiten Hauptsatz existieren unterschiedliche Versionen (Cápek & Sheehan, 2005), von denen die meisten das Temperaturkonzept beinhalten. Da die NPE auch bei Abwesenheit von Temperatur vorhanden ist, setzt eine Analyse der Möglichkeit zur Gewinnung von NPE eine Version des Zweiten Hauptsatzes voraus, die keine Temperatur zur Voraussetzung hat. Plancks Version des Zweiten Hauptsatzes besagt: „Jeder … Prozess, der sich in der Natur ereignet, läuft in der Weise ab, dass sich die Summe der Entropien aller beteiligten Körper … erhöht.“ Da Arbeit (einschließlich elektrischer Energie) eine Entropie von null aufweist, würde die Umwandlung einer entropiehaltigen Energiequelle, z. B. Wärme, gegen den Zweiten Hauptsatz verstoßen, es sei denn, die überschüssige Entropie wird über einen Wärmeverlust abgeführt. Die Entropie ist ein Maß für die Anzahl der Optionen, die ein System der Energieverteilung zur Verfügung stellt. Die NPE stellt im freien Raum den einzigen Grundzustand dar, die einzige Möglichkeit, und besitzt daher null Entropie (Boyer, 2002). Aus diesem Grund steht es uns frei, die NPE im freien Raum in Arbeit umzuwandeln, ohne gegen den Zweiten Hauptsatz zu verstoßen.

Anders verhält es sich bei einem Casimir-Hohlraum, dessen Entropie ungleich null ist und die einen Bezug zum Hohlraumabstand aufweist (Revzen et al., 1997). Wird der Hohlraumabstand im Zuge der Energieentnahme variiert, z. B. über die Nutzung der Casimir-Kraft zur Erzeugung von Arbeit, dann ändert sich die Entropie des Systems. Um die Notwendigkeit zu vermeiden, die Entropie des Systems verringern zu müssen und somit die Plancksche Version des Zweiten Hauptsatzes zu verletzen, müsste also Wärme abgeführt werden, um auf diese Weise Entropie abzutragen. Dies würde die Menge an NPE, welche in Arbeit umgewandelt werden könnte, einschränken – soweit dies überhaupt möglich ist. In dem hier beschriebenen System zur Gewinnung von NPE kommt es jedoch zu keinerlei Änderung des Hohlraumabstandes und somit auch zu keiner Änderung der inneren Entropie. Daher lässt sich die NPE in Arbeit umsetzen, ohne dass es zwangsläufig zu einer Verletzung des Zweiten Hauptsatzes kommen muss.

Sollte also aus den Fluktuationen des Quantenvakuums tatsächlich NPE gewonnen werden können, dann stellt sich die entscheidende Frage nach der Natur der ihr zugrunde liegenden Energiequelle:

• Die NPE ist fester Bestandteil der Quantenmechanik, was zu der beunruhigenden Vorstellung führt, dass die Menge an NPE in einem geschlossenen System gleich bliebe, auch wenn man diesem System NPE entnehmen würde. Die Entnahme von NPE würde dann gegen den Energieerhaltungssatz, den Ersten Hauptsatz der Thermodynamik, verstoßen, selbst wenn sie nicht gegen den Zweiten Hauptsatz verstoßen würde.

• Eine alternative Auffassung von NPE beschreibt die stochastische Elektrodynamik (Boyer, 1975), eine faszinierende, jedoch unvollständige klassische Alternative zur Quantenmechanik, bei der der Raum von echter elektromagnetischer NPE erfüllt ist, welche sich dynamisch zwischen Materie und Raum hin und her bewegt. Ein Modell der stochastischen Elektrodynamik würde die Extraktion von NPE ermöglichen, ohne den Ersten oder Zweiten Hauptsatz der Thermodynamik zu verletzen.

• Schließlich spekuliere ich auf ein „thermisches Modell“, in dem die Quelle für NPE letztendlich thermischer Natur ist. Die NPE und die thermische Energie sind eng miteinander verbunden (Boyer, 2012), doch die Vorstellung, dass es zwischen diesen beiden Gebilden zu einem Energieaustausch kommt, wird mit Sicherheit nicht akzeptiert werden. Sollte sich allerdings zeigen, dass die Entnahme von NPE aus einem System letztlich die thermische Energie dieses Systems anzapft, dann würde die Entnahme von NPE zu einer Abkühlung des Systems führen, was einen Verstoß gegen gleich mehrere Versionen des Zweiten Hauptsatzes bedeuten würde.

Sollten unsere Bauelemente tatsächlich durch NPE gespeist werden, könnte eine Untersuchung des Prozesses der Energieentnahme dazu beitragen, die eigentliche Quelle für diese Energie zu ermitteln.

Fazit

Machen wir uns etwas vor? Wir haben zahlreiche Tests darauf überprüft, ob es sich bei ihren Ergebnissen um Artefakte handelt, und sie waren allesamt negativ (eine kurze Beschreibung dazu finden Sie in Anhang II). Vor kurzem haben mehrere Institute, die für ihre Messgenauigkeit bekannt sind, unsere Bauelemente in einer streng kontrollierten Umgebung getestet und dabei die von uns gemessenen Werte reproduziert (noch nicht veröffentlicht). Über Dutzende von verschiedenen Testläufen und Tausende von Messungen hinweg konnten wir konsistente Trends feststellen.

Was wir beobachten, ist Realität – doch worauf ist diese zurückzuführen? Ich streite ständig mit mir selbst und mit jedem, der sich einbringt, darüber, ob die zu beobachtende Energieerzeugung auf die NPE zurückzuführen ist oder ob es da noch eine andere Quelle gibt. Die Ausgangsleistung setzt einen angrenzenden optischen Hohlraum voraus und variiert im umgekehrten Verhältnis zur Stärke des Hohlraumes, was mit der NPE als Quelle im Einklang steht. Die Leistung variiert ebenfalls mit der Stärke des Isolators sowie der oberen Elektrode in einer Weise, die wiederum mit der Photoinjektion im Einklang steht. Jüngste Beobachtungen haben gezeigt, dass der Effekt sich mit abnehmender Temperatur nicht verringert (noch nicht veröffentlicht), was gleichfalls für die NPE als Quelle spricht.

Die Theorie der Quantenelektrodynamik ist bezüglich des Quantenvakuums und der NPE sehr stringent, allerdings in Bezug auf die Natur der NPE immer noch nicht eindeutig. So werden nach wie vor neue Eigenschaften des Casimir-Effektes entdeckt. In Anbetracht des sich entwickelnden Charakters unseres Verständnisses von der NPE stellt sich die Frage: Muss hier die Theorie vorangehen und das Experiment folgen? Betrachtet man die Geschichte des wissenschaftlichen Fortschritts, so würde ich dies bestreiten. „Wir sollten die grundlegende Tatsache nicht aus den Augen verlieren, dass es sich bei den wichtigsten experimentellen Ergebnissen gerade um solche handelt, für die es keine theoretische Interpretation gibt.“ (Anderson, 1990).

Wieso gibt es trotz all der verschiedenen Ansätze, die bereits vorgeschlagen wurden (Moddel & Dmitriyeva, 2019), noch keine weiteren eindeutigen Beobachtungen zur Gewinnung von NPE? Besteht die Möglichkeit, dass sich meine Vermutungen als richtig erweisen, nach denen der Schlüssel darin zu suchen ist, die Energie im Femtosekundenbereich einzufangen, und dass unsere Bauelemente (soweit wir dies beurteilen können) mit der einzigartigen Fähigkeit ausgestattet sind, die Energie auf so schnelle Weise zu gewinnen und einzufangen?

Ein faszinierendes Abenteuer. Von noch größerer Bedeutung ist jedoch die Tatsache, dass die Technologie, sollten diese Bauelemente tatsächlich in der Lage sein, die NPE zu gewinnen, die Zukunft einer Welt, die dringend eine saubere und vergleichsweise günstige Energiequelle benötigt, wirklich grundlegend verändern könnte. Die Bauelemente, die wir derzeit fertigen, sind zwar winzig, doch hat die Technologie dieser Bauelemente bereits wiederholt ihre Fähigkeit zur Hochskalierung unter Beweis gestellt. Sollte auch nur ein Bruchteil der von mir berechneten Leistung von 5 GW/m2 aus dem Quantenvakuum zur Verfügung stehen, könnte damit die gesamte Menge an Energie bereitgestellt werden, die in absehbarer Zukunft von uns benötigt wird.

Danksagung

Mein Dank gilt Ayendra Weerakkody, Dave Doroski und Dylan Bartusiak, dem Team, das die in Moddel (2021a) beschriebenen Bauelemente entworfen, gefertigt und getestet hat, als auch den jüngeren Mitgliedern des Teams, Bradley Pelz und Kyuyoung Bae. Ich bedanke mich bei Matt McConnell und Swapnil Mhatre für ihre Kommentare zu meinem Manuskript. Ohne die Ermutigung und die Unterstützung von Matt McConnell wäre dieses Unterfangen nicht möglich gewesen. Ein Großteil der Arbeit wurde von der Denver Foundation unterstützt, wofür ich sehr dankbar bin, und in jüngerer Zeit von der Radanta Corporation.

Referenzen

Anderson, P. (1990). Solid-state experimentalists: Theory should be on tap, not on top. Physics Today, 43(9), 9–10. physicstoday.scitation.org/doi/10.1063/1.2810678

Bhansali, S., Krishnan, S., Stefanakos, E., & Goswami, D. Y. (2010, December). Tunnel junction based rectenna – A key to ultrahigh efficiency solar/thermal energy conversion. In AIP Conference Proceedings, 1313(1), (pp. 79–83). American Institute of Physics. aip.scitation.org/doi/pdf/10.1063/1.3530572

Boyer, T. H. (1975). Random electrodynamics: The theory of classical electrodynamics with classical electromagnetic zero-point radiation. Physical Review D, 11(4), 790. journals.aps.org/prd/abstract/10.1103/Phys-RevD.11.790

Boyer, T. H. (2002). Connecting blackbody radiation and zero-point radiation within classical physics: A new minimum principle and a status review. arXiv preprint physics/0206033. arxiv.org/abs/physics?0206033

Boyer, T. H. (2012). The blackbody radiation spectrum follows from zero-point radiation and the structure of relativistic spacetime in classical physics. Foundations of Physics, 42(5), 595–614. link.springer.com/content/pdf/10.1007/s10701-012-9628-x.pdf

Cápek, V., & Sheehan, D. P. (2005). Challenges to the second law of thermodynamics (pp. 202–203). Springer. link.springer.com/book/10.1007/1-4020-3016-9

Casimir, H. B. (1948). On the attraction between two perfectly conducting plates. In Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, 51 (p. 793).

Davies, P. C. W., & Ottewill, A. C. (2002). Detection of negative energy: 4-dimensional examples. Physical Review D, 65(10), 104014.

Fertig, H. A. (1990). Traversal-time distribution and the uncertainty principle in quantum tunneling. Physical review letters, 65(19), 2321.

Ford, L. H. (1991). Constraints on negative-energy fluxes. Physical Review D, 43(12), 3972.

Ford, L. H. (2022). Electric field and voltage fluctuations in the Casimir effect. Physical Review D, 105(6), 065001.

Grover, S., & Moddel, G. (2012). Engineering the current-voltage characteristics of metal-insulator-metal diodes using double-insulator tunnel barriers. Solid-State Electronics, 67(1), 94–99. sciencedirect.com/science/article/abs/pii/S0038110111003224

Hecht, E. (2017). Optics, Fifth Edition. Pearson.

Huang, H., & Ford, L. H. (2015). Quantum electric field fluctuations and potential scattering. Physical Review D, 91(12), 125005. DOI: 10.1103/PhysRevD.91.125005

Jaeger, G. (2019). Are virtual particles less real? Entropy, 21(2), 141. mdpi.com/1099-4300/21/2/141

Kingbury, K. (2009). The Casimir Effect. aphyr.com/media/comps.pdf

Kragh, H. (2012). Preludes to dark energy: Zero-point energy and vacuum speculations. Archive for History of Exact Sciences, 66(3), 199–240. link.springer.com/article/10.1007/s00407-011-0092-3

Milonni, P. W. (2013). The quantum vacuum: An introduction to quantum electrodynamics. Academic Press.

Moddel, G., & Dmitriyeva, O. (2019). Extraction of Zero-Point Energy from the vacuum: Assessment of stochastic electrodynamics-based approach as compared to other methods. Atoms, 7(2), 51. mdpi.com/2218-2004/7/2/51

Moddel, G., Weerakkody, A., Doroski, D., & Bartusiak, D. (2021a). Optical-cavity-induced current. Symmetry, 13(3), 517. mdpi.com/2073-8994/13/3/517

Moddel, G., Weerakkody, A., Doroski, D., & Bartusiak, D. (2021b). Casimir-cavity-induced conductance changes. Physical Review Research, 3(2), L022007. journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.3.L022007

Moddel, G. (2021c). U.S. Patent No. 11,133,758. Washington, DC: U.S. Patent and Trademark Office. patents.google.com/patent/US11133758B2/en

Revzen, M., Opher, R., Opher, M., & Mann, A. (1997). Casimir’s entropy. Journal of Physics A: Mathematical and General, 30(22), 7783.

Rivera, N., Wong, L. J., Joannopoulos, J. D., Soljačić, M., & Kaminer, I. (2019). Light emission based on nanophotonic vacuum forces. Nature Physics, 15(12), 1284-1289. nature.com/articles/s41567-019-0672-8

Stahlhofen, A. A., & Nimtz, G. (2006). Evanescent modes are virtual photons. EPL (Europhysics Letters), 76(2), 189. iopscience.iop.org/article/10.1209/epl/i2006-10271-9/pdf

Wilson, C. M., Johansson, G., Pourkabirian, A., Simoen, M., Johansson, J. R., Duty, T., ... & Delsing, P. (2011). Observation of the dynamical Casimir effect in a superconducting circuit. Nature, 479(7373), 376–379. nature.com/articles/nature10561.pdf

Yang, Y., & Kawazoe, Y. (2012). Characterization of zeropoint vibration in one-component crystals. EPL (Europhysics Letters), 98(6), 66007. iopscience.iop.org/article/10.1209/0295-5075/98/66007/pdf

Anhang I: Berechnung der Stromstärke und der Leistung, die das Quantenvakuum bereitstellt

Hier werden die verfügbare Stromstärke und Leistung abgeleitet, wie sie sich aus der elektromagnetischen Hintergrundstrahlung des Quantenvakuums ergeben. Ich beginne mit der Energiedichte der elektromagnetischen Moden im Raum, [math]\rho(hf)[/math], wie in Gleichung (1) angegeben. Obwohl der Vakuumzustand nur über virtuelle Photonen verfügt (Milonni, 2013), lässt sich eine grobe Berechnung zur Flussdichte von NPE-Photonen, welche auf eine Oberfläche treffen, wie folgt durchführen. Der Fluss ist gleich der Energiedichte geteilt durch die Photonenenergie [math]hf[/math] mal der Photonengeschwindigkeit [math]c[/math]. Genau wie beim klassischen Stefan-Boltzmann-Gesetz für Schwarzkörperstrahlung muss ein geometrischer Faktor von [math]^1/_4[/math] eingerechnet werden. Der Photonenfluss pro Frequenzeinheit ergibt sich dann wie folgt:

[math]j = \rho(hf) \frac{c}{4hf}[/math] .

(2)

Um den über einen Frequenzbereich verfügbaren Gesamtfluss zu ermitteln, wird der Ausdruck [math]\rho(hf)[/math] aus Gleichung (1) in Gleichung (2) eingesetzt und der Fluss bis zu einer Grenzfrequenz [math]f_{co}[/math] integriert. Behält man nur den rechten eingeklammerten NPE-Term [math]hf/2[/math] aus Gleichung (1) bei, so beträgt der Gesamtfluss:

[math]\Delta J = \frac{\pi}{c^2} \int^{f_{co}}_{0} f^2df = \frac{\pi}{3h^3c^2} (hf_{co})^3[/math] .

(3)

Dieser kumulierte Photonenfluss ist beträchtlich. Bei einer Grenzenergie von 4 eV beträgt er beispielsweise 1028 Photonen m-2 s-1, was einem Photonenstrom von 1,7 GA m-2 entspricht, wobei der Photonenstrom als der elektrische Strom definiert ist, der erzeugt werden würde, wenn jedes einfallende Photon den Strom eines Elektrons erzeugen würde. Um die verfügbare kumulative Leistung zu berechnen, wird der Photonenstrom für jede Energie in dem Integral in Gleichung (3) mit der Photonenenergie multipliziert:

[math]P = \frac{\pi}{c^2} \int^{f_{co}}_{0} hf^3df = \frac{\pi}{4h^3c^2} (hf_{co})^4[/math] .

(4)

Bei einem einheitlichen Grenzwert von 4 eV beträgt die verfügbare Leistung 5,0 GW m-2.

Anhang II: Überprüfung auf Artefakte

Eine ausführliche Erörterung zu einem Großteil der Überprüfungen auf Artefakte findet sich in Moddel et al. (2021a), sofern nachfolgend keine anderen Referenzen aufgeführt sind.

So stellt sich unter anderem die Frage, ob es sich bei den beobachteten Ergebnissen nur um einen kurzfristigen Effekt handelt, der auf eine Aufladung der Oberflächen oder auf eine chemische Reaktion zurückzuführen ist. Um dies zu überprüfen, haben wir die Stromabgabe kontinuierlich über 4 Stunden und später über 24 Stunden gemessen, um zu schauen, ob sie abnimmt. Würde beispielsweise jedes Molekül des Isolators eine Ladung einfangen, dann könnten diese den beobachteten Strom für die Dauer von 3 μs erzeugen. Wir konnten allerdings keine Veränderung in der Leistungsabgabe feststellen, auch nicht über den Zeitraum von 24 Stunden. Was wir beobachtet haben, stellt also keinen vorübergehenden Effekt dar.

Sollte das, was wir beobachtet haben, auf die Gewinnung von Strom über die aktive Fläche des Bauelementes zurückzuführen sein und nicht etwa auf Energie, welche aus einem anderen Teil des Schaltkreises stammt, dann sollte der Strom mit der Fläche des Bauelementes skalieren. Wir konnten feststellen, dass der Strom für Flächen von 6 bis 10 000 μm2 mit der Fläche skaliert. In ähnlicher Weise sollte die Leistung mit der Anzahl der Bauelemente pro Baugruppe skalieren. Wir fanden heraus, dass zwei unterschiedliche Typen von 4×4-Anordnungen die vierfache Menge an Strom und eine viermal so hohe Spannung erzeugen wie einzelne Bauelemente, womit also die erwartete Skalierung eingetreten war.

Eine weitere Frage besteht darin, ob die Ausgangsleistung tatsächlich auf den angrenzenden optischen Hohlraum zurückzuführen ist oder ob sie aus der Art und Weise resultiert, wie die MIM-Struktur im Anschluss an ihre Fertigung bearbeitet wurde, um den angrenzenden Hohlraum zu schaffen. Wir haben die Bauelemente in drei verschiedenen Stadien ihrer Fertigung bis hin zur Einbringung des transparenten Dielektrikums in den Hohlraum gemessen und dabei keinen Ausgangsstrom feststellen können – erst nach dem die abschließende Spiegelschicht aufgebracht worden war, kam es zur Leistungsabgabe. Somit ist die Leistung nicht auf einen Fehler in der Verarbeitung zurückzuführen, sondern kommt erst durch das fertiggestellte Bauelement zustande.

Es bestehen allerdings verschiedene Möglichkeiten dafür, dass die beobachtete Leistungsabgabe auf die unabsichtliche Aufnahme von Ladungen oder elektromagnetischen Feldern zurückzuführen ist:

• Um zu ermitteln, ob der Strom möglicherweise auf Ladungen auf dem Spiegel zurückzuführen ist, die bis zur MIM-Struktur vorgedrungen sind, haben wir den Widerstand des optischen Hohlraumes mit dem der MIM-Struktur verglichen. Für sämtliche Stärken des optischen Hohlraumes konnten wir feststellen, dass der Widerstand des Hohlraumes mindestens eine Million Mal so hoch war wie der der MIM-Struktur, so dass eine Ladung, die sich versehentlich auf dem Spiegel gebildet hat, nicht in jenen Bereich der MIM-Struktur vordringen konnte, über den wir den Strom gemessen haben (siehe Abbildung 3(a)).

• Kürzlich haben wir untersucht, ob eine an den Spiegel angelegte Spannung in der Lage ist, einen Feldeffekt zu erzeugen, welcher einen Strom durch die MIM-Struktur hindurch induziert. Selbst bei Spiegelspannungen von bis zu 10 V konnten wir keine Auswirkungen auf den MIM-Strom feststellen (Weerakkody, unveröffentlicht 2022).

• Um zu überprüfen, ob elektromagnetische Störungen vorliegen, haben wir die I(U)-Kennlinien eines Bauelementes in einer Mu-Metall-Box, welche niedrige Frequenzen blockiert, sowie in einer Aluminiumbox, welche höhere Frequenzen blockiert, gemessen und dabei keine Veränderungen im Vergleich zu den Bauelementen festgestellt, die unter normalen Umgebungsbedingungen gemessen wurden.

Thermoelektrische Spannungen, also Spannungen in Folge von Temperaturdifferenzen zwischen verschiedenen Positionen auf einem Bauelement oder innerhalb eines Messsystems, bilden für Messungen im niedrigen Leistungsbereich eine große Herausforderung. Es wurden drei verschiedene Tests durchgeführt, um mögliche thermoelektrische Spannungen zwischen dem Bauelement und dem Messsystem zu ermitteln:

• Um derartige Spannungen zu kompensieren, wurden die meisten Messungen mittels einer Methode der Spannungsumkehr durchgeführt, die wie folgt umgesetzt wird: Es werden zwei Messungen mit Strömen von entgegengesetzter Polarität durchgeführt, also eine Messung, bei der die Basiselektrode geerdet ist, und eine weitere, bei der die obere Elektrode geerdet ist, und dann wird die Differenz zwischen beiden Strömen errechnet, auf beide Messwerte angewandt und so der endgültige Wert erhalten.

• Die Tatsache, dass die oben beschriebenen 4×4-Anordnungen das Vierfache der Ausgangsspannung eines einzelnen Bauelementes liefern, weist darauf hin, dass diese Spannung nicht auf thermoelektrische Spannungen zwischen dem Bauelement und dem Messsystem zurückzuführen ist, da diese nicht mit der Anzahl der in Reihe geschalteten Bauelemente skalieren würde.

• Unlängst wurden erste Messungen durchgeführt, für die die Temperatur des Bauelementes von etwa Raumtemperatur (300 K) auf rund 80 K gesenkt wurde, und dabei wurden hinsichtlich der Ausgangsleistung des Bauelementes nur geringe Abweichungen festgestellt, die sich aber alle im Rahmen des experimentellen Fehlerbereiches bewegten (Weerakkody, unveröffentlicht 2022).

Zur Überprüfung, ob die Ergebnisse auf Temperaturgradienten im Inneren des Testobjektes zurückzuführen sein könnten, haben wir zwei Tests durchgeführt:

• Die Temperaturdifferenz zwischen der Umgebung oberhalb der Bauelemente und dem Messtisch wurde variiert, und es konnte keine Veränderung der Leistung festgestellt werden.

• Die Bauelemente wurden in einem geschlossenen Kryostat unter Einhaltung einer exakt gleichbleibenden Temperatur gemessen, und es wurde auch hier keine Veränderung der Leistung festgestellt (Weerakkody, unveröffentlicht 2022).

Aus den dargelegten Gründen erscheint es unwahrscheinlich, dass die von uns beobachteten Ergebnisse auf einen thermoelektrischen Effekt zurückzuführen sind.

Die Berechnungen zum erwarteten Strom, wie er sich aus der Absorption bekannter Ströme von kosmischer Strahlung und von solaren Neutrinos ergeben würde, hatten nicht die Mengen an Strom zum Ergebnis, die von uns beobachtet wurden.

Zusammenfassend lässt sich sagen, dass wir alle in Frage kommenden Artefakte untersucht haben, welche als Quelle für die beobachtete Stromerzeugung durch unsere Bauelemente in Betracht kamen, und dass keines davon eine Erklärung für die Ergebnisse liefern konnte.